Айзек Азимов - Популярная физика. От архимедова рычага до квантовой механики

Представим себе вновь плоское зеркало. Пучок параллельных лучей падает на него вдоль главной оси (за главную ось на плоском зеркале можно принять любую линию нормали) и отражается обратно вдоль нее таким же параллельным. Лучи не встречаются, и соответственно расстояние от зеркала до фокуса бесконечно. Но если f бесконечно, то 1/f должно быть равным нулю, и для плоского зеркала уравнение 2.2 принимает вид:

Если решить уравнение 2.4 для D 1, то выходит, что D 1= –D 0 . Так как D 0(расстояние до отражаемого объекта) всегда должно быть положительно, поскольку для того, чтобы вообще отражаться, предмет должен всегда находиться перед зеркалом, D 1должно быть отрицательным. Соответственно в случае плоского зеркала изображение всегда должно находиться за зеркалом и быть мнимым. Итак, если D 1, и D 0не равны, то изображение должно находиться далеко за зеркалом, в то время как отражаемый объект находится перед зеркалом.

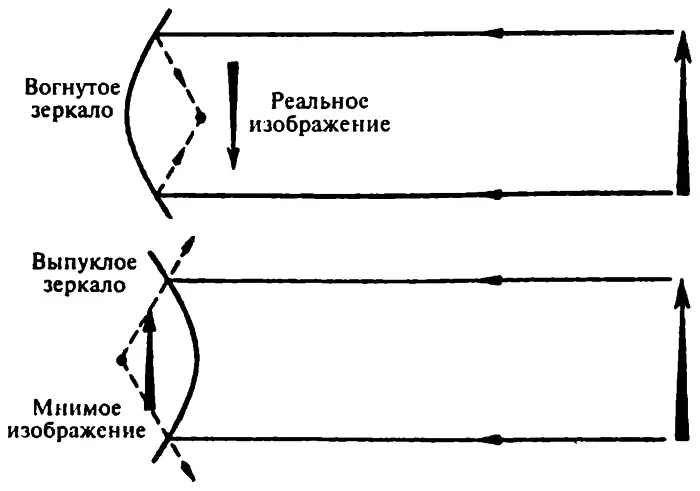
А что, если у нас выпуклое зеркало? То есть кривое зеркало, посеребренное с вогнутой стороны, так что мы, глядя в него, видим отражение с выпуклой стороны. Пучок параллельных лучей света падает на такое зеркало и отражается в стороны от главной оси (за исключением одного луча, который совпадает с ней). Опять же, если расходящиеся отраженные лучи продолжить (мысленно) сквозь зеркало, они сойдутся в фокусе.

Фокус выпуклого зеркала, лежащий за зеркалом, является мнимым фокусом, расстояние от него до зеркала отрицательно. Поэтому, говоря о выпуклом зеркале, мы должны говорить о –f и соответственно о –1/f. Для выпуклого зеркала уравнение 2.2 приобретает вид:

Поскольку отражаемый предмет должен быть всегда перед зеркалом, D 0и соответственно 1/D 0 должны быть положительными. Следовательно, 1/D 1— 1/f должно быть положительным, а чтобы это было так, 1/D 1должно быть больше, чем 1/f. Но это уводит нас еще на шаг дальше и говорит о том, что само по себе D 1должно быть меньше, чем f. Другими словами, очевидно, что расстояние до мнимого изображения, отраженного выпуклым зеркалом, должно быть меньше фокусного, как бы далеко от зеркала ни находился отраженный объект. По этой причине все объекты, отраженные в выпуклом зеркале, кажутся сжатыми в крошечное пространство, и маленькое выпуклое зеркало в углу большой переполненной комнаты может дать панорамный обзор всей комнаты (хотя и в несколько искаженном виде).

Размеры изображения (S 1) зависят от размеров отражаемого объекта (S 0), так же как зависят друг от друга и расстояния, вне зависимости от того, простираются ли они вперед или назад по отношению к зеркалу. Иными словами,

На плоском зеркале, где расстояние от изображения до зеркала равно расстоянию от зеркала до отражаемого объекта, размеры объекта и изображения равны. Плоское зеркало не уменьшает и не увеличивает объект. В выпуклом зеркале, где все изображения должны быть ближе к зеркалу, чем фокус, как бы далеко ни были отображаемые объекты, все изображения маленькие. Чем дальше находится отражаемый объект, тем ближе и соответственно меньше изображение.

В вогнутом же зеркале, когда отражаемый объект лежит между фокусом и центром изгиба, изображение находится за центром изгиба. В таком случае, поскольку изображение находится дальше от зеркала, чем отражаемый объект, изображение крупнее, чем объект. Чем ближе объект находится к фокусу, тем крупнее получается изображение. Разумеется, чем изображение крупнее, тем оно тусклее, поскольку одно и то же количество света распространяется на все большую площадь.

Свету не обязательно быть отраженным, чтобы отклоняться от прямолинейного движения. Проходя из одной прозрачной среды в другую, скажем из воздуха в воду, свет, скорее всего, не отразится, а будет продолжать движение, тем не менее направление изменить может.

Несомненно, сначала это было замечено первобытным человеком, когда он обнаружил, что палка, которую положили одним концом в воду, кажется согнутой в том месте, где она входит в воду. Однако, если ее достать, она снова оказывается прямой.

Опять же, можно положить предмет на дно пустой чашки и посмотреть на чашку под таким углом, чтобы предмет был только-только скрыт краем чашки. Если теперь налить в чашку воду, то предмет на дне станет видимым, хотя ни он, ни наблюдающий глаз не переместились. Уже во времена древних греков было понятно — чтобы объяснить это, придется признать, что свет изменил направление при переходе из одной прозрачной среды в другую.

Представьте себе плоский кусок чистого стекла, совершенно прозрачный, и представьте себе луч света, пылающий на него по нормали, то есть падающий на стекло ровно под прямым углом к его плоской поверхности. Если вы приглядитесь, то обнаружите, что свет проходит сквозь стекло, не меняя направления.

Теперь представьте, что свет падает на стекло косо, под углом i к нормали. Можно предположить, что свет будет просто продолжать движение сквозь стекло, оставаясь под тем же углом i к нормали внутри стекла. Однако это не так. Луч света искривляется в точке, где воздух соприкасается со стеклом (на границе воздуха и стекла). Более того, он искривляется по направлению к нормали таким образом, что новый угол, который он образует к нормали внутри стекла (r), меньше, чем угол падения i.

Эта смена направления луча света при переходе от одной прозрачной среды к другой называется преломлением, или рефракцией (что по-латыни значит «перелом»). Угол r является, разумеется, углом преломления.

Если угол падения уменьшается или увеличивается, угол преломления тоже уменьшается или увеличивается. Но каким бы ни было значение i , значение r всегда будет меньше.

Физики древности считали, что угол преломления прямо пропорционален углу падения и, следовательно, удвоение i всегда будет приводить к удвоению r. Это почти так, пока мы говорим о небольших углах, но, если углы становятся больше, этот «закон» обнаруживает свою несостоятельность.

Предположим, например, что свет падает под углом 30° к нормали, попадая на границу стекла с воздухом, а угол преломления, с которым свет попадает в стекло, равен 19,5°. Если угол падения удваивается и становится равным 60°, то угол преломления становится равным 35,3°. Угол преломления возрастает, но не удваивается.

Истинное соотношение между i и r было обнаружено сначала в 1621 году голландским физиком Виллебордом Снеллом (1591–1626). Он не опубликовал свое открытие, и французский философ Рене Декарт (1596–1650) открыл его заново в 1637 году, опубликовав его в той форме, в которой мы сейчас его и знаем (эта форма гораздо более проста, чем форма, которую предлагал Снелл).