Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Это свойство независимости периода колебаний маятника от амплитуды носит мудреное название изохронность — от греческого слова «изохронный», означающий «равновременный». Мы говорим, что движение маятника при малых амплитудах (приблизительно) изохронно. Это свойство заслуживает специального названия, ибо оно оказалось весьма ценным.

В приведенной ниже задаче 1 проводятся рассуждения, позволяющие перейти от маятника к другим системам, в которых совершаются изохронные колебания. Задача довольно сложная, но ее стоит попытаться решить, ибо она может служить примером задач по теоретической физике. Разбор задачи покажет вам, как от простого опытного факта перейти к предсказанию новой области технических знаний. Если вы успешно справились с «анализом движения маятника», проведенным в задаче 1 , значит, вы сможете подыскать и другие системы, которые совершают изохронные колебания и еще больше подходят для регулирования хода часов.

Действительно, революция в измерении времени, началом которой послужило предложение Галилея, продолжается. Она прошла путь от больших часов с маятником до карманных и наручных часов с балансом и спиральной пружиной, колеблющихся кристаллов кварца, а теперь в качестве нового этапа — колебательных и вращательных движений самих атомов.

Закончите «теоретический анализ» колебаний маятника [155], который проведен ниже.

Задача 1

Опыт показывает, что при малых амплитудах период колебаний Т практически не зависит от амплитуды. Анализируя движение маятника, мы будем ограничиваться только малыми амплитудами. При удвоении амплитуды период колебания маятника Т остается неизменным, хотя груз проходит вдвое большее расстояние. Следовательно, чтобы амплитуда стала вдвое больше, груз должен двигаться быстрее.

Скорость движения не постоянна, даже ускорение не остается постоянным. Однако изменение скорости груза происходит одинаково при разных амплитудах, поэтому мы можем высказать предположение, что, будучи неодинаковой на разных стадиях отклонения, скорость груза на соответствующих стадиях движения с удвоенной амплитудой должна быть больше, чем скорость движения с первоначальной амплитудой, иначе Т не оставалось бы неизменным.

Задача 2

Отважившись на обобщение рассуждений, проведенных в задаче 1 , мы должны ожидать, что при любых (малых) амплитудах скорости на соответствующих стадиях колебания связаны с амплитудой колебания следующим образом: ___

Задача 3

Вернемся к задаче 1 , где сравнивались колебания, амплитуда которых отличаются вдвое. Поскольку удвоение амплитуды равносильно увеличению соответствующих скоростей ___ и поскольку груз приобретает эти скорости за один и тот же промежуток времени [156], его ускорение Δ v /Δ t при удвоенной амплитуде должно быть ___ больше, чем при колебании с первоначальной амплитудой. (Опять-таки ускорение не остаётся постоянным, но мы сравниваем ускорения на соответствующих стадиях колебания.)

Задача 4

Обобщая рассуждения в задаче 3 , можно сказать, что соотношение между ускорением (на любой выбранной стадии колебания) и амплитудой должно выглядеть следующим образом: ___.

Задача 5

Хотя в конце отклонения груз не движется, он обладает наибольшим (направленным к вертикали) ускорением. Это ускорение обусловлено совместным действием силы тяжести и силы, приложенной к грузу со стороны нити. Эти силы в сумме дают результирующую силу F , направление которой совпадает с направлением движения. Из задачи 4 представляется правдоподобным, что результирующая сила, действующая на груз в конце отклонения, должна быть связана с амплитудой А следующим образом [157]: ___

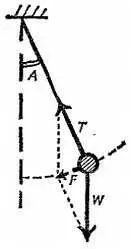
Фиг. 259. К задаче 5.

Задача 6

Это соотношение между силой и отклонением от положения равновесия должно выполняться на любой стадии колебания. Это выглядит похожим на ___

Задача 7

Исходя из задачи 6 , мы можем ожидать, что движение, при котором период Т не зависит от амплитуды, будет наблюдаться для таких тел, как ___, причем для этих тел независимость периода от амплитуды, по всей вероятности, должна быть

_______________________

(ограничена малой амплитудой? не ограничена? или?)

Простое гармоническое движение

Все изохронные колебания представляют собой движения одного и того же типа с одинаковым по форме графиком зависимости амплитуды от времени — синусоидой . Мы называем такое движение простым гармоническим движением (эпитетом «гармоническое». Это движение обязано тому важному значению, которое оно имеет в музыке). Колебания маятника при малых отклонениях очень близки к простым гармоническим движениям. Груз, подвешенный на пружине, движется вверх и вниз, совершая при этом простые гармонические движения в широких пределах изменения амплитуды. (Проделайте наскоро опыт в лаборатории: он доставит вам большое удовлетворение.) Пружина с подвешенным грузом, гибкий брус, растягиваемая проволока, закручиваемый стержень, любая упругая система, подчиняющаяся закону Гука , совершает колебательное движение, называемое простым гармоническим колебанием .

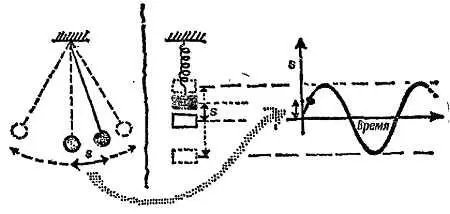
Фиг. 260. Изохронные колебания и график зависимости смещения от времени.

«Простым гармоническим движением» мы называем повторяющееся движение особого типа — движение маятника и схожее с ним движение груза на пружине, — это не просто любое движение с постоянным периодом. (Кроты, выползающие из-под земли каждое утро в поисках пищи и возвращающиеся каждую ночь обратно под землю, совершают в известном смысле «изохронное» движение — его период составляет 24 часа, как бы ни были глубоки их норы, — но это, разумеется, отнюдь не простое гармоническое движение.) Если проанализировать движение маятника, обратившись к геометрии, то можно установить важную характеристику этого движения.

Движение маятника характеризуется переменным ускорением , которое всегда направлено к среднему положению и изменяется прямо пропорционально расстоянию от этого положения.

Если s — расстояние вдоль траектории, скажем, груза маятника, а а — ускорение, то мы найдем a ~ s , или а= —k 2 s, где k — вещественная постоянная.

Знак минус показывает, что ускорение направлено в сторону, противоположную отклонению. (Когда груз отклонен вправо — мы считаем такие отклонения положительными, когда ускорение направлено влево, мы приписываем ему отрицательное значение.)