Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

3. Это проекция кругового движения , совершаемого с постоянной скоростью (например, круговое движение, каким оно представляется при наблюдении в плоскости круга, или движение тени, которую отбрасывает на землю тело, движущееся по окружности, лежащей в вертикальной плоскости, при освещении вертикальным солнечным светом).

4. Это движение, в случае которого график зависимости смещения от времени представляет собой синусоиду .

Математика, а также простые соображения из механики в первом определении показывают, что во всех случаях происходит одно и то же движение. Чтобы связать воедино приведенные определения, здесь требуется лишь проделать некоторые выкладки и указать на ряд опытов.

Значение простого гармонического движения

Простое гармоническое движение играет такую же важную роль в описании природы, как движения с постоянной скоростью и с постоянным ускорением, поскольку:

1. Этот вид движения весьма распространен (примерами могут служить маятники, музыкальные инструменты, колеблющиеся детали машин, океанские приливы, переменные токи, свет, соответствующий определенной линии спектра).

2. Период этого движения не зависит от амплитуды (благодаря этому оно используется для измерения промежутков времени).

3. Это движение поддается простому математическому описанию

s= A∙sin k t

откуда следует формула

T= 2π/ k

где

k 2= (Жесткость пружины )/( Масса ).

Так можно предсказать величину Т . В других случаях измеряют Т и с помощью полученного значения подсчитывают жесткость пружины.

4. Согласно теореме Фурье, любое периодическое движение можно разложить на простые гармонические составляющие (см. ниже). Разложение легко выполняется методами математического анализа (когда исходное — периодическое движение описывается какой-либо формулой) или с помощью вычислительной машины (когда исходный процесс представлен только графиком). Поэтому на основе простого математического описания гармонических движений можно рассматривать значительно более сложные движения: движение волн в гавани, музыкальные звуки, издаваемые кларнетом, речевые колебания, сейсмические волны…, движения электронов в атоме. Что касается звуков, то наши органы слуха, по-видимому, производят «гармонический анализ» и разлагают сложный звук на чистые тоны.

Гармонический анализ

Теорема Фурье настолько всеобъемлюща, что трудно указать пределы ее приложения. Она не ограничивается периодическими движениями или повторяющимися процессами. Вот несколько примеров:

а) На фиг. 269 приведен график звуковых колебаний, создаваемых флейтой. Результат анализа кривой в очевиден: она представляет собой сумму сигналов, в которой значительная доля приходится на колебания а и содержится некоторая доля колебаний б . (Если подуть чуть сильнее, возникнет комбинация исходного тона и одного из его октавных повторений — обертонов — приятный музыкальный звук, хотя и необычный для флейты.)

Фиг. 269. Графическое изображение звуковых колебаний, создаваемых флейтой.

а— при нормальной игре; б— воздушная струя большой силы дает октавное повторение звука; в— воздушная струя несколько сильнее нормальной.

б) В радиотехнике можно без труда получить «прямоугольную волну» и продемонстрировать ее на экране осциллографа. (Форму прямоугольного сигнала может иметь, например, кривая, описывающая звук, издаваемый «щелкунчиком» с металлическими челюстями, которые быстро раскрываются, и резко смыкаются.) На фиг. 270 представлена попытка произвести гармонический анализ прямоугольного сигнала. Основная составляющая имеет такую же «длину волны», как и прямоугольный сигнал. В некоторых местах она выступает за пределы исходной кривой, а в других — не доходит до нее, и эти несоответствия формы должны быть компенсированы. Следующая составляющая должна иметь «длину волны», равную 1/3 основной, т. е. втрое большую частоту. Расхождения, остающиеся после этой составляющей, в значительной мере устраняются добавлением небольшой по амплитуде составляющей, у которой частота в 5 раз больше частоты исходной кривой, и т. д.

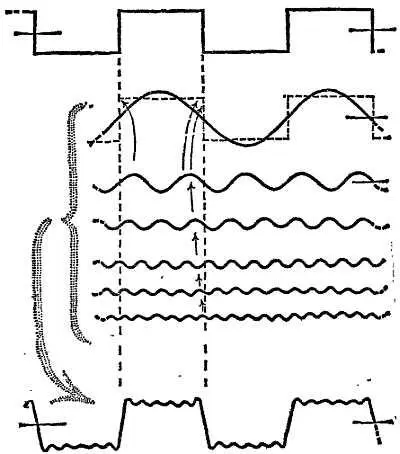
Фиг. 270. Разложение прямоугольного сигнала на гармонические составляющие.

Заметьте, что даже при большом числе гармоник результирующая кривая (сумма) обнаруживает нежелательные острые выбросы.

Для точного описания необходим бесконечный ряд составляющих, отношение частот которых к частоте исходной кривой равно 1, 3, 5, 7… Однако даже сумма нескольких первых составляющих дает удовлетворительное приближение (если не считать нежелательных выбросов на вершине). Так мы получаем удобный способ проверки динамиков, микрофонов и т. д. На прибор подают прямоугольный сигнал. Если прибор хорошо воспроизводит форму прямоугольного сигнала, это значит, что он способен пропускать как очень высокие, так и весьма низкие частоты.

в) Речевые колебания часто имеют сложную форму. На фиг. 271 показана довольно простая по форме кривая, которая представляет собой графическое изображение звука «у…», произносимого нараспев. Вы можете предсказать результат разложения этого колебания на гармонические составляющие: основной тон + тон значительно более высокой частоты, который мы считаем характерным для данного гласного звука. Такой анализ чрезвычайно важен для инженеров: им пользуются при проектировании систем телефонной связи, по которой передается речь, при разработке экономичных преобразователей речевых колебаний в кабельной телефонии и высококачественных приемников, предназначенных для воспроизведения речи. Произнесенные нараспев другие гласные звуки или недостаточно искусные певцы вызывают гораздо более сложные с виду колебания, но эти колебания тоже можно без труда разложить на несколько основных составляющих.

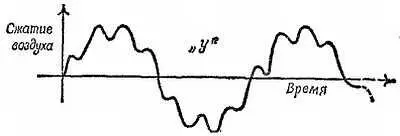
Фиг. 271. Кривая звука « у…».

г) «Волновой пакет». Гармонический анализ можно применить к одиночному импульсу (ему соответствует звук от шлепка или радиоволна, испускаемая при ударе молнии) и к короткому цугу волн, вроде волнообразного всплеска, которым в современной теории характеризуют положение движущегося электрона. Для идеального представления таких сигналов приходится складывать составляющие, которые образуют бесконечный набор частот, но составляющие с заметной амплитудой равномерно распределены в пределах полосы частот вокруг исходной частоты.