Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Масса атома водорода равна

0,00000000000000000000000000166 кг.

Чтобы избавиться от одного нуля, нужно умножить это число на 10. Чтобы избавиться от всех двадцати шести нулей, нужно умножить его на 10 26, тогда получим 0,166. Умножение еще на 10 дает 1,66. Таким образом, чтобы получить число 1,66, следует передвинуть запятую на 27 разрядов вправо, т. е. произвести умножение на 10 27. Но масса атома должна остаться неизменной, значит, нужно разделить 1,66 на 10 27. «Разделить на 10 27» записывают как «умножить на 10 -27», следовательно, масса атома водорода равна 1,66 х -27кг.

Один килограмм гелия содержит

1500000000000000000000000000 атомов гелия.

В стандартной форме это число будет записано в виде 1,5 х 10 27.

Чтобы перемножить числа, записанные в стандартной форме, нужно перемножить их «главные части» на линейке и сложить оба показателя степени числа 10 — сумма показателей даст новый показатель степени десяти.

Чтобы разделить одно число на другое, нужно вычесть из одного показателя степени числа 10 другой. Например,

a) (3,1 x 10 4)x(2,0 x 10 3) = 6,2 x 10 4+3= 6,2 x 10 7,

б) (3,1 x 10 -4)х(2,0 x 10 +1) = 6,2 x 10 -4+1= 6,2 x 10 -3

в) 3,1 x 10 4/2,0 x 10 3 = 1,55 х 10 4–3= 1,55 х 10 1

г) 3,1 x 10 -4/2,0 x 10 +1 = 1,55 х 10 -4-1 = 1,55 х 10 -5

д) 3,1 x 10 -4/2,0 x 10 -7 = 1,55 х 10 -4-(-7) = 1,55 х 10 +3

е) (3,1 x 10 -4х 6,0 x 10 7)/(2,0 x 10 -3 х 1,55 x 10 2) = 6,0 х 10 -4+7-(-3)-2=

= 6,0 х 10 -4+7+3–2= 6,0 х 10 4

Счетная линейка

Счетная линейка позволяет легко и быстро умножать и делить числа, если научиться оценивать доли мелких делений линейки. Но линейка ничего не говорит о том, где должна стоять запятая. Чтобы установить положение запятой, нужно либо проделать грубый подсчет в уме, либо записать все числа, над которыми производятся действия, в стандартной форме и после этого сделать приближенный расчет. Например, требуется вычислить

(126 x 79,2 x 0,074)/(0,00521 x 876)

Линейка дает 1618. Грубый подсчет дает

(120 х 80 х 7/ 100)/( 5/ 1000х 800), или (120 х 7)/5, или примерно 160

Поэтому запятую следует поставить так: 161,8.

Стандартная запись дает

Следовательно, ответ 161,8.

Проценты

Знак % означает просто 1/ 100, так что 2 % означает 2/ 100; 6,21 % означает 6,21/ 100, a 0,03 % означает 0,03/ 100. Если вы хотите, например, выразить 3/ 20с помощью знака %, то нужно превратить 3/ 20 в равновеликую дробь со знаменателем 100. В данном случае это просто: 3/ 20 — это то же самое, что 15/ 100. Значит, 3/ 20 равно 15 %, т. е. 15 % — это просто иной способ записи дроби 3/ 20 !

Чтобы перевести в % число 3,2/ 23, мы должны перевести его в равновеликую дробь со знаменателем 100. Для этого запишем 3,2/ 23 в виде дроби со знаменателем 1, после чего умножим числитель и знаменатель на 100. Производя затем деление в числителе, получаем

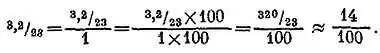
Значит, 3,2/ 23— это то же самое, что дробь 14/ 100, которую мы записываем в виде 14 %. Выразить 3 в процентах от 20 означает просто записать дробь 3/ 20и превратить ее в равновеликую дробь со знаменателем 100, а затем записать новую дробь с помощью знака %. Мы записываем 3/ 20в виде 15/ 100, следовательно, ответ 15 %.

Чтобы выразить 0,032 в процентах от 7,91, мы записываем дробь 0,032/ 7,91и преобразуем ее так, чтобы числитель и знаменатель были целыми числами: 32/ 7910. Затем превращаем эту дробь в дробь со знаменателем 100 и получаем

Запись ошибок экспериментальных данных в процентах

Если результаты двух измерений какой-нибудь величины несколько отличаются друг от друга, то их расхождение выражают в процентах от всего результата измерений. Так сделано в приводимых ниже примерах:

1) Экспериментаторы А и В фиксируют время на соревнованиях, они получили соответственно 506 и 504 сек. Разница в замерах 2 сек, ее нужно отнести к результату самих замеров, который немногим превышает 500 сек. Чтобы указать, насколько близко оба результата совпадают, мы выражаем их разность в виде доли всего времени: 2 сек/500 сек. Разность 2 сек составляет 2/ 500замеренного времени. Превращая эту дробь в дробь со знаменателем 100, получаем 2/ 500= 0,4/ 100= 0,4 %. Мы говорим, что результаты измерений различаются на 0,4 %.

2) Два взвешивания одного и того же предмета дают 2,130 и 2,132 кг. Оба взвешивания различаются на 0,002 кг, эту разницу нужно отнести к результату взвешивания, равному 2 кг. Таким образом, интересующая нас дробь равна 0,002/ 2, или 0,001, т. е. 0,1 %. Мы говорим, что расхождение результатов взвешивания составляет 0,1 %.

Считая оба измерения одинаково надежными, (допустим, что они произведены двумя хорошо успевающими учащимися), мы можем выразить в процентах их расхождение , но это нельзя называть ошибкой в процентах. Если же экспериментатор проверяет новый прибор, измеряя с его помощью какую-либо известную величину, то расхождение между полученным результатом и стандартным значением можно выразить в процентах. Полученную таким образом величину можно назвать ошибкой (в процентах) и приписать ее прибору. Иногда проделывают много измерений той или иной величины и берут среднее из полученных результатов, рассчитывая таким путем исключить случайные ошибки. При этом можно выразить в процентах разности между отдельными результатами и средним значением и назвать их ошибками отдельных измерений, выраженными в процентах.

«Ошибка» (в процентах) характеризует небрежность при выполнении эксперимента или недостатки приборов, она свидетельствует о неопределенности в аппаратуре или в наших рассуждениях. Стремиться к чрезмерной точности при указании ошибок нет смысла. Это нелогично. Например, если разрубить обеденный стол на дрова, то вряд ли стоит потом зачищать куски дерева наждачной бумагой! Допустим, что, вычисляя ошибки, мы получили величину 0,4219365 %. Представлять ошибку таким числом — совершенно неразумно; так никогда не поступают. Если же указать, что ошибка равна 0,4 %, то это вполне имеет смысл, таким числом можно пользоваться.

Поэтому безразлично, на какое число мы будем делить при подсчете процентной ошибки: на один из результатов измерений, на их среднее или на какое-то близкое к ним округленное число . Выражая в процентах ошибку, т. е. недостаток точности, стараться вычислить ее как можно точнее — это просто тратить впустую время. В приведенном выше втором примере можно делить 0,002 на 2,130, или 2,132, или просто на 2. Ответы будут такие:

0,002/2,130 = 0,0939 %, 0,002/2,132 = 0,0938 %, 0,002/2 = 0,1000 %.

Все три результата дают при округлении одно и то же значение 0,1 %. Именно этим значением, легко вычисляемым в уме, и стал бы пользоваться любой физик.

Вычисления с ошибками

Предположим, что для вычисления какой-то величины требуется перемножить несколько результатов измерений. Для нахождения ошибки произведения нужно сложить все ошибки (или неопределенности) сомножителей. При этом ошибку произведения, как и ошибки сомножителей, выражают в процентах. Например, допустим, что при измерении площади прямоугольного участка землемер по небрежности находит завышенные значения длины и ширины. Предположим, что измеренная им длина завышена на 2 %, а ширина — на 3 %. Результат вычисления площади участка будет завышен на 2 + 3 %, т. е. на 5 %, а не на 2 x 3 %, что составляет 0,06 %. Предлагаем вам разобрать следующие задачи.