Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Задача 1. Ошибки в сомножителях

а) ( Арифметическая задача .) Длина прямоугольного участка 400 м, а ширина 300 м. Измерения выполнены неточно, они дали значения 408 м на 309 м.

Вычислите истинную площадь поля.

Вычислите площадь поля по результатам измерений.

Выразите ошибку, допущенную при измерении длины участка, в процентах от длины. Найдите также ошибку в процентах, допущенную при измерении ширины.

Выразите ошибку в определении площади участка в процентах от площади.

Чтобы найти площадь участка, мы умножаем его длину на ширину. Какое правило нужно применить для определения ошибки, допущенной при вычислении площади в приведенном примере? Как мы должны поступить: перемножить ошибки, допущенные при измерении длины и ширины участка, или сложить эти ошибки?

б) ( Более формальный подход .) Рассмотрите задачу следующим образом:

Результат определения длины

408 м или (400) + (2 % от 400).

Мы можем записать это в виде

400 + ( 2/ 100)∙400

и представить произведением 400∙(1 + 2/ 100)

Точно так же запишите ширину участка. Вычислите площадь участка по полученным результатам измерений, перемножив длину и ширину, записанное в виде произведений:

(400∙(1 + 2/ 100))∙(300 + ())

Это дает

400∙300∙()()

или

120 000∙()()

Величина 120 000 кв. м характеризует истинную площадь. Поэтому произведение ()(), будучи представлено суммой (1 + некоторое число), прямо дает ошибку в процентах при определении площади. Преобразуйте произведение ()() к сумме вида (1 + некоторое число), как это делается в алгебре. Точно так же, как запись 400∙(1 + 2/ 100) указывает ошибку 2 % в измерении длины, 400 м, результат такого преобразования покажет, что ошибка в определении площади равна…%.

в) ( Алгебраический вариант .) Размеры прямоугольного земельного участка X м на Y м. Длина участка завышена при измерении на x % и равна по данным измерений Х + ( x /100)∙ Х м; ширина завышена на у %.

Разложите длину и ширину, найденные при измерениях, на множители, как в задаче ( б ). Перемножьте обе величины, чтобы найти площадь. В полученном результате нужно выделить ту часть, которую можно истолковать как ошибку в процентах, допускаемую при определении площади. [Обратите внимание на то, что ошибка не равна в точности величине, вычисляемой по приведенному выше простому правилу. Произведение ()(), приведенное к сумме (1 + некоторое число), содержит еще одну очень малую дробь со знаменателем 10 000. Эта дробь представляет собой чрезвычайно малую добавку к ошибке, и ею можно пренебречь. Убедитесь в этом сами, подставив конкретные числа; например, возьмите 2 вместо х и 3 вместо у .]

г) ( Геометрический вариант .) Нарисуйте прямоугольный участок поля. Удлините стороны прямоугольника так, чтобы длина увеличилась на х %, а ширина — на у %, и очертите новые границы участка. Какую долю первоначальной площади составляют добавочные полоски?

Задача 2. Ошибки в сомножителях со знаками плюс и минус

Предположим, что в задаче 1 при обмере участка длина оказалась завышенной, а ширина заниженной. Покажите в общем виде с помощью алгебраических преобразований или на примере с конкретными числами, что ошибка в процентах при вычислении площади равна разности ошибок в определении длины и ширины или алгебраической сумме этих ошибок, если ошибку заниженного результата измерений считать отрицательной.

Задача 3. Ошибки в двух и более одинаковых сомножителях

Предположим, что прямоугольный участок в приведенных выше задачах представляет собой квадрат. Если землемер это знает, он измеряет лишь одну сторону квадрата X (с ошибкой х %) и для определения площади возводит результат измерения в квадрат.

1. Какова ошибка в процентах при таком подсчете площади?

2. Вообще если произведение содержит сомножитель X 2, то ошибка х % сомножителя X приводит к ошибке в произведении, равной…%.

3. Если произведение содержит величину X 3, то ошибка х % сомножителя X приводит к ошибке в произведении, равной…%.

4. Если произведение содержит величину X n, то ошибка х % сомножителя X приводит к ошибке в произведении, равной…%.

Задача 4. Ошибки в квадратных корнях

Предположим, что произведение содержит в качестве множителя √ Х .

Как повлияет ошибка в X , равная х %, на точность произведения? Попытайтесь сообразить, какой будет ответ, воспользовавшись одним из следующих способов:

1. Запишите √ Х в виде X 1/2и примите в качестве допущения, что правило решения четвертого вопроса задачи 3 применимо и в том случае, когда n — дробное число.

2. Если множитель √ Х фигурируете произведении дважды, то мы получаем √ Х ∙√ Х , или (√ Х ) 2, т. е. X . Значит, ошибка в X , равная х %, дает ошибку х % в произведении. Поэтому если множитель √ Х встречается только один раз, то мы полагаем, что ошибка составит… %.

…текст не читается…

сталкиваются, например, при разделении изотопов урана для получения атомной энергии. См. задачу в гл. 30 [169].)

Задача 5. Ошибки в делителях

Предположим, нам нужно вычислить частное X / Y . Если значение Y завышено на у %, то как это отразится на частном? Предположим, мы увеличили X на столько же процентов, что и Y . Тогда частное будет, равно

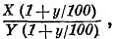
или X / Y , т. е. не изменится. Если знаменатель дроби завышен на у %, то эта ошибка в точности компенсирует ошибку у % в числителе, который тоже завышен. Обе ошибки дают одинаковый по величине и противоположный по знаку вклад в ошибку частного. Следовательно, если завысить на у % знаменатель дроби, то это приведет к такому же результату, как занижение на у % числителя. Значит, ошибка + у % в делителе Y приведена к ошибке частного X / Y , равной — у %. Заметьте, что это следует и из решения четвертого вопроса задачи 3 .

Задача 6. Вычисление результата с несколькими множителями

Предположим, эксперимент приводит к результату

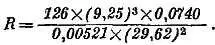
Экспериментаторы дают для своих измерений следующие ошибки в процентах:

от точного значения 126 может отличаться на ±1 %,

9,25 — на ±0,2 %,

0,0740 — на ±0,1 %,

29,62 — на ±0,2 %,

0,00521 — на ±0,1 %.

Если бы все результаты отдельных измерений были занижены на величину ошибки, то

а) числитель записанной выше дроби R был бы занижен на…?…%,