Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

Знаки

Результат измерения, погрешность которого экспериментатор считает равной 0,001, может быть записан тремя способами:

x = 3,1642 ± 0,003,

x = 3,1642 ± 0,1 %,

x = 3,164.

В третьей строчке последняя цифра 4 рассматривается как недостоверная. Ниоткуда не следует, что цифра 4 отличается от верной на ±3. Эта форма записи дает лишь основание считать, что последняя цифра сомнительна — обычно такой записи достаточно, чтобы указать на имеющуюся погрешность. В двух предыдущих строчках появление последней цифры 2 совершенно неоправдано: ошибка показывает, что такая запись результата (с точностью до последней цифры 2) лишена смысла. Экспериментатор, сохраняющий эту цифру, обманывает сам себя.

Если эксперимент дает приближенное значение или приближенный ответ появляется в результате оценки, не следует записывать результат как х = 800, ибо это противоречит точному смыслу знака =. Вместо этого нужно писать

х 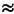(~=) 800.

Такая запись означает их приближенно равно 800». Символ обычно означает «приблизительно равно» (хотя это утверждение не совсем логично).

При более грубой оценке можно написать

у ~ 1000.

Это значит, что у ближе к 1000, чем к 100 или к 10 000. Подобная грубая оценка «порядка величины» часто имеет огромное значение.

Так было с оценкой размера атома столетие назад, так обстоит дело с определением радиуса Вселенной (если он вообще не бесконечен) в наши дни. Во многих случаях достаточно произвести измерение с точностью до порядка величины. Например, когда речь идет о росте температуры, достаточно малом, чтобы им можно было пренебречь, или о весе, заведомо настолько большом, что поверхностное натяжение можно считать несущественным, то же самое можно сказать об определении приближенной даты исторического события, когда излишнее уточнение даты только отвлекает внимание от сущности события.

Если результаты представлены в стандартной форме, например

z = 2,34 х 10 6и w = 7,8 х 10 3

то их порядки величины будут

z ~ 10 6и w ~ 10 4.

Вы несомненно найдете применение знакам в своей работе, чем бы вы ни занимались, и привыкнете проводить между ними различие. Заметьте, что символы эти не вполне установившиеся. Некоторые авторы и издатели заменяют символ другими знаками.

Пропорциональная зависимость — ключ ко многим законам

Выражая наши знания о природе в виде простых законов, мы прежде всего ищем постоянство в явлениях: масса тела остается постоянной, полный электрический заряд тоже, количество движения сохраняется неизменным, все электроны одинаковы. Почти столь же простой и плодотворный принцип выражает прямая пропорциональность между величинами, при которой две измеряемые величины возрастают в одинаковой пропорции: удлинение пружины при увеличении нагрузки, сила и ускорение, давление и плотность газа.

Мы говорим, что для пружины (в пределах действия закона Гука)

УДЛИНЕНИЕ пропорционально НАГРУЗКЕ

или

УДЛИНЕНИЕ изменяется прямо пропорционально [171]НАГРУЗКЕ.

Это записывают в виде

УДЛИНЕНИЕ ~ НАГРУЗКА.

Как и процентам, в элементарных курсах часто отводят особое место пропорциям и функциональной зависимости, и эти понятия кажутся чем-то таинственным и труднодоступным. Не будь этого, их считали бы очевидными с точки зрения здравого смысла. Рассмотрим несколько простых примеров.

Пример В . Предположим, что при снабжении картофелем некоего лагеря недельные потребности определяются следующим образом:

для лагеря на 100 человек требуется 200 кг картофеля

… 200… 400…

… 300… 600…

… 500… 1000…

Масса картофеля возрастает пропорционально размерам хозяйства. Это простейший тип соотношения между двумя величинами, с которым мы так часто встречаемся в физике [172].

Можно сформулировать это соотношение несколькими способами:

1) МАССА КАРТОФЕЛЯ пропорциональна ЧИСЛУ ЛЮДЕЙ;

2) МАССА КАРТОФЕЛЯ изменяется прямо пропорционально ЧИСЛУ ЛЮДЕЙ;

3) МАССА КАРТОФЕЛЯ ~ ЧИСЛУ ЛЮДЕЙ (это сокращенная запись формулировок 1 и 2);

4) МАССА КАРТОФЕЛЯ = (ПОСТОЯННАЯ)∙(ЧИСЛО ЛЮДЕЙ).

Варианты 1 и 2 (и их математическая запись — вариант 3) — это просто попытки дать формулировку простым в очевидным вещам. « Две величины возрастают в одинаковой пропорции . Если удвоить одну из них, то удваивается вторая, если утроить одну, — утраивается вторая, и т. д.».

Имея это в виду, можно легко решать задачи, не вычисляя «постоянную», содержащуюся в записи варианта 4. Например, известно, что для 100 человек требуется 200 кг картофеля. Сколько потребуется его для 600 человек? Для вшестеро большего числа людей требуется в 6 раз больше продовольствия: 1200 кг.

Пример Г .Объем шара изменяется пропорционально третьей степени радиуса . Шар увеличен так, что радиус его стал в 5 раз больше первоначального. Что произойдет с его объемом? Если радиус увеличивается в 5 раз по сравнению с первоначальным, то величина (радиус) 3возрастает в 5 3раз по сравнению с первоначальным значением (поскольку R 3= R∙ R∙ Rи 5 R∙5 R∙5 R= 5 3∙ R 3). Следовательно, объем возрастает По сравнению с первоначальным в 125 раз. Это должно быть следствием здравого смысла, дли которого вовсе не нужно обращаться к соотношению 4/3π R 3.

«Коэффициент пропорциональности»

Формулировка 4

МАССА КАРТОФЕЛЯ = (Постоянная)∙ЧИСЛО ЛЮДЕЙ

очень похожа на запись варианта 3, но для специалиста формулировка 4 не столь четко выражает идею зависимости между величинами. Поэтому советуем избегать ею пользоваться, если только можно получить нужный результат, прибегнув к здравому смыслу, как в приведенных выше двух примерах.

Для каждой пары значений в примере с картофелем, очевидно, справедливо соотношение

МАССА КАРТОФЕЛЯ Р= 2 N∙ЧИСЛО ЛЮДЕЙ,

поэтому все четыре случая можно описать с помощью формулы P= 2 N. Сущность этой записи в том, что она выражает зависимость между величинами: дело не в конкретном значении 2, а в том, что это число остается одним и тем же, т. е. постоянным . (Фактически это потребление картофеля, приходящееся на одного человека, т. е. 2 кг на человека.) Поскольку число 2 постоянно, мы можем записать

Р= (Постоянная)∙ N.

Эта общая формулировка применима и к случаю, когда в лагерь собираются люди, потребляющие много картофеля, и на одного человека уходит уже 5 кг картофеля. Тогда наша форма примет вид P = 5∙ N. (Конечно, если одни обитатели лагеря съедают по 2 кг картофеля в неделю, а другие по 5 кг, то вся схема рассуждений теряет силу. Надо иметь в виду, что такая же опасность существует и при выводе научных законов).