Эрик Роджерс - Физика для любознательных. Том 3. Электричество и магнетизм. Атомы и ядра

Фиг. 193. Получение и анализ спектров.

Если белый свет из раскаленного твердого тела проходит через холодный газ, то мы можем наблюдать «спектр поглощения»: полный спектр белого света с черными линиями, в которых свет отсутствует, при длине волны, на которой газ излучал бы свет, если бы он был раскален. Эти линии поглощения можно использовать для анализа атмосферы вокруг «твердых» звезд, в том числе и нашего Солнца, в спектре белого света у которых наблюдаются темные линии, характерные для водорода, паров натрия, кальция и т. д. Эти линии, очевидно, получаются из-за того, что атомы более холодного газа поглощают свет, который соответствует их «собственным колебаниям» [194]. Они должны затем снова испускать точно такой же свет, но уже во всех направлениях, так что линия выглядит темной по сравнению с другими цветами, которые приходят непосредственно из более горячей «сердцевины» звезды. Эти факты снова наталкивают на мысль о некотором механизме колебаний, способном реагировать на волны определенной частоты.

Фиг. 194. Эскизы спектров.

Эти черно-белые эскизы — только тусклая имитация. Взгляните на реальные вещи: посмотрите на неоновую вывеску через призму или дифракционную решетку; держите блестящую швейную иглу на солнце и рассматривайте ее через призму, которую следует держать близко к глазам, — вы увидите фраунгоферовские линии поглощения. (В реальных спектрах линий обычно гораздо больше, чем изображено здесь. Относительная яркость линий зависит от условий возбуждения атомов.)

Далее, было ясно, что атомы, возбужденные бомбардировкой или электрическим полем, могут колебаться и испускать волны света с различными частотами. Есть ли сходство между этими собственными «естественными частотами» атома и колеблющейся струной? Струна арфы или скрипки может колебаться с любой частотой из некоторой серии в соответствии с тем, что стоячая волна имеет одну пучность или 2, 3, 4… пучности. Тогда частоты находятся в той же самой пропорции, т. е. 1:2:3:4:…, а издаваемые музыкальные ноты имеют соответствующие частоты.

Для струны теория согласуется с экспериментом. Второй закон Ньютона предсказывает серию:

ЧАСТОТА = ( постоянная К)∙( n),

где n = 1, 2, 3… Частоты света разных цветов в спектре атома водорода образуют почти столь же простую серию, формула для которой (из эксперимента) имеет такой вид:

ЧАСТОТА = ( постоянная К)∙((1/2 2) — (1/ n 2))

где n = 3, 4, 5… для последовательных линий серии. Точные измерения [195]с помощью высококачественной дифракционной решетки дали значение

К = 3290 000 000 000 000.

Бор предсказал эту формулу с постоянной К , равной

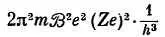
(см. следующий раздел). При использовании измеренных величин h, е, m и Z = 1, = 9,00∙10 9эта формула дает

К = 3 286 000 000 000 000.

В более полной форме предсказание Бора выглядело так:

v= K∙((1/ n f 2) — (1/ n i 2))

где n f— «конечное» квантовое число для орбиты, на которую «падает» электрон, одинаковое для всех линий серии, а n iозначает «начальное» квантовое число другой орбиты, с которой «падает» электрон.

Видимой серии для водорода соответствует n f = 2 и n i= 3, 4, 5…

Задача 4

Две другие серии для водорода были уже известны, а еще две были открыты позднее там, где их предсказал Бор. Посмотрите на приведенную выше общую формулу и предскажите формулу для серии в ультрафиолетовой области с большими квантами и для серии вблизи инфракрасной области.

Другие элементы после возбуждения также дают линейчатые спектры, если они находятся в газообразном состоянии. При расшифровке большинства линейчатых спектров можно использовать почти ту же самую константу К , а остальная часть формулы имеет довольно похожую алгебраическую форму. Поэтому с точки зрения предположений Бора все линейчатые спектры приобретают следующий смысл: каждая линия образуется в результате того, что электрон «перепрыгивает» с одной разрешенной орбиты (или «уровня») на другую, испуская разность энергий в виде кванта света этой спектральной линии. Сами по себе орбиты, определенные квантовыми правилами, стабильны: электрон может оставаться длительное время на одной из них, не излучая. В этом причина того, что (холодный) газ не светится до тех пор, пока его не облучат. Излучение испускается лишь при изменении орбит. Поэтому, чтобы электрон мог испускать свет, он должен сначала двигаться по внешней орбите, т. е. находиться на высоком энергетическом уровне и иметь возможность «упасть» на низший уровень. И в этом же причина того, что атомы газа испускают резкие спектральные линии, каждая из которых имеет определенную длину волны, поскольку получается при переходе между определенными орбитами. Таким образом, спектры создаются возбужденными атомами. Ион (атом, потерявший электрон), получая обратно потерянный электрон, может испускать одну или последовательно несколько линий, когда этот электрон «падает» с одного энергетического уровня на другой.

Сегодня понятие «стабильные орбиты» звучит слишком категорично, но мы будем использовать лишь их существенное свойство — определенность энергии на каждой из них — и поэтому будем говорить об «уровнях энергии».

Так Бор преобразовал спектроскопию, которая была эмпирической схемой исследования газов, в важное средство изучения атомной структуры.

Фиг. 195. Размещение линий спектров по шкале частот.

а— проанализированный по сериям спектр гелия; б— видимые серии атомарного водорода.

Спектроскопическая постоянная по Бору. Примите на веру или вычислите сами

Предсказание постоянной К требует математических выкладок для вычисления энергии электрона в поле ядра. Примите на веру результаты таких выкладок, приведенные на математической схеме (фиг. 196), или проследите за приведенными ниже вычислениями.

Фиг. 196. Схема математических расчетов для атома Бора.

Нам нужно знать энергию электрона для квантовых чисел n = n iи n = n f. Тогда мы сможем предсказать частоту измеряемого фотона, поскольку

h∙ vизлучения = Δ E= Δ E i— Δ E f.

Электрон, движущийся по орбите, имеет энергию Е , складывающуюся из кинетической энергии (К. Э.) и потенциальной энергии (П. Э.) (которая равна энергии, накопленной в электрическом поле системы электрон + ядро). Перенесем электрон из бесконечности на расстояние r от ядра с зарядом Z e . Он притягивается ядром, поэтому при сближении электрона с ядром энергия переходит от электрического поля к электрону (в виде кинетической энергии).