Эрик Роджерс - Физика для любознательных. Том 3. Электричество и магнетизм. Атомы и ядра

Такая точка зрения объясняет, в частности, почему атом не может сжиматься так, чтобы электроны двигались по все меньшим и меньшим орбитам. Если положение каждого электрона действительно описывается стоячей волной, то на длине окружности наименьшей орбиты должна укладываться ровно одна длина волны — немыслимо, чтобы в кольцевой стоячей волне содержалась только часть длины волны, — которая должна определить минимальный размер, до которого можно сжать атом. (Соответствующее ограничение для простейшей стоячей волны остается справедливым и при замене циркулярных «орбит» более общими картинами.)

Некоторый смысл приобретает и принцип Паули: посадите несколько тождественных электронов на одну и ту же «орбиту» — картины их стоячих волн сложатся в одну-единственную картину, и тогда мы можем ожидать, что обнаружим один электрон вместо нескольких [203].

Новая атомная теория

Мощный аппарат был развит Шредингером. Исходя из дебройлевского квантово-волнового постулата, он составил общее волновое уравнение (см. т. 2, стр. 588) для электронов. Затем он посмотрел, какие решения в форме стоячих волн должны соответствовать полю кулоновских сил, меняющихся по закону обратных квадратов внутри атома. Это аналогично следующему: определить скорость волны вдоль натянутой струны (см, гл. 10 : СКОРОСТЬ 2= НАТЯЖЕНИЕ / МАССА НА ЕДИНИЦУ ДЛИНЫ); подставить ее в общее волновое уравнение ( 2 V= (1/ c 2)∙( d 2V/ dt 2)); наложить «граничные условия», как, например, для жестко закрепленной струны длиной L (закреплены концы, что предотвращает движение в точках х = 0 и x = L ); затем найти частоты возможных стоячих волн (как в гл. 10 , где вычислены частоты для 1 пучности, 2 пучностей и т. д.). В случае, который рассматривал Шредингер, частоты по квантовому правилу дают энергии. Волновые уравнения и граничные условия здесь более сложны, чем для струны, но они приводят к ценным результатам.

Эта новая интерпретация вскоре была математически применена к волновому рассмотрению электронов в атомах, которое далеко превосходит в успешных предсказаниях теорию Бора. Как и рассмотрение Бора, оно оказалось успешным в применении к атому водорода, даже с более тонкими деталями, и, сверх того, в применении к сложным атомам. Рассмотрение перераспределения электронов при химических превращениях в волновом описании также дало правильные предсказания. Волновое описание было успешно распространено на ядерную физику и интерпретировало радиоактивность в терминах волн-частиц, которые просачиваются через потенциальный барьер ядра. Все это — ценой отказа от какой-либо наглядно определенной модели или картины. Картина атома Бора содержала необязательные конкретные детали — недоказуемые экспериментально и, следовательно, недопустимые для любой долговременной научной теории. Теперь четкие орбиты исчезают и заменяются математическими формулировками волновой модели, которые дают определенные уровни энергии, в точности соответствующие энергиям электронов на старых боровских орбитах. Но у нас нет картины соответствующих волн. Кроме математической формулировки, у них нет ничего общего с волнами на воде или с волнами света. В нашем новом рассмотрении используются такие волны, интенсивность которых показывает, где с наибольшей вероятностью должен быть электрон. Интенсивность волны в выбранной области показывает, сколько шансов за то, что здесь находится электрон. Об интерферирующих световых волнах мы говорим, что математическое описание сообщает нам шансы того, что фотон попадает в определенную часть картины: самые низкие шансы соответствуют темной полосе, самые высокие — светлой. Для связанных электронов в стабильных состояниях атомов у нас есть утверждение о стоячих волнах, которые описывают только облако вероятности распределения электронов: наиболее вероятно здесь, вероятно там, менее вероятно во всех других местах.

Точно так же облако вероятности имеется внутри радиоактивного ядра, например для группы нуклонов α -частицы: вероятность того, что α -частица находится внутри, велика, но, так как волны вероятности распределены во всем пространстве, у α -частицы имеются некоторые шансы оказаться снаружи. В один прекрасный момент она воспользуется этими шансами; тогда она уже снаружи, и после этого электрическое поле выбрасывает ее вдаль. Это грубое, вульгаризованное «объяснение» радиоактивности.

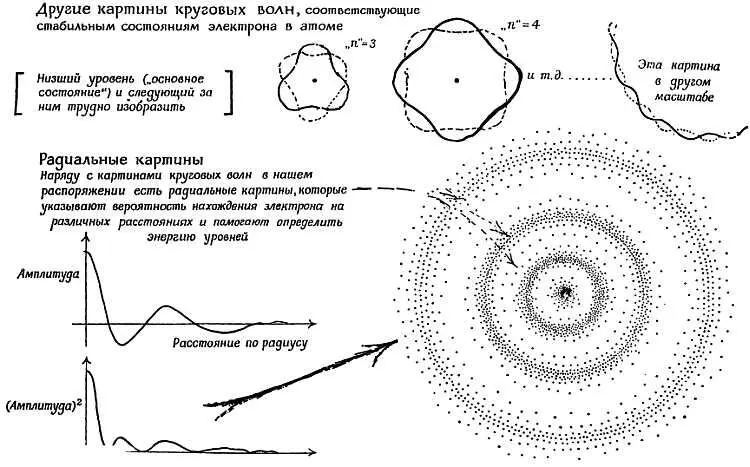
Фиг. 207. Другие волновые картины атомных моделей.

Фиг. 208.

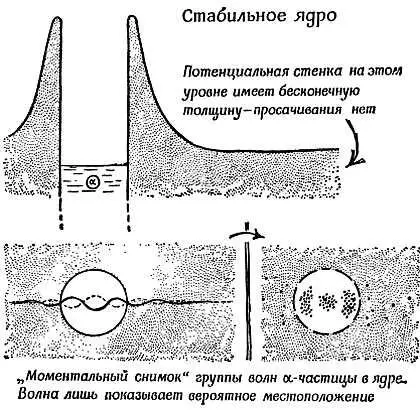
Фиг. 209. Волновые картины в ядрах.

Новое рассмотрение атомов оказалось точным, но отнюдь не простым. При более детальной разработке идея о волнах становится более плодотворной, но сами волны от этого не становятся более реальными. Для их описания мы имеем хороший математический аппарат, но не имеем модели для интерпретации результатов. По существу модели оказались обреченными на неудачу, поскольку они часто вводят в заблуждение. Наша картина атомов и их поведения осталась математической моделью — сложной моделью с зацепляющимися друг за друга частями, которая приводит к плодотворным результатам. Поэтому мы вверяем атомную теорию математикам. Они развили новые средства, например сложную алгебру с нетривиальными правилами [204]. Несмотря на странность методов, результаты превосходны и во всех перечисленных ниже пунктах подтверждаются экспериментальными проверками:

Волновой формализм дает для сложных атомов уровни энергии и вероятности нахождения электрона на каждом уровне; это приводит к успешным предсказаниям частот спектральных линий и их яркостей.

При описании молекул как комбинации атомов волновой формализм предсказывает химические энергии и силы поверхностного натяжения. Он даже предсказывает углы и расстояния между атомами в длинных молекулярных цепях, что подтверждается измерениями с помощью рентгеновских лучей.

Вычисленные вероятности нахождения электрона в некоторой области определенного атома согласуются с измерениями рассеяния потока электронов на атомных электронах в мишени из таких атомов.

Кинетическая энергия α -частиц сообщает нам их длину волны. Это дает вероятность их просачивания через ядерный барьер, что позволяет с определенным успехом предсказать период полураспада радиоактивного ядра.