Эрик Роджерс - Физика для любознательных. Том 3. Электричество и магнетизм. Атомы и ядра

б— интерференционная картина, образованная электронами (увеличено в 5000 раз).

Фотография Г. Мёлленштедта и X. Дюкера из Тюбингенского университета. Эксперимент опубликован в журнале «Zeitschrift fur Phisik», том 145, 1956.

Сложный конфликт

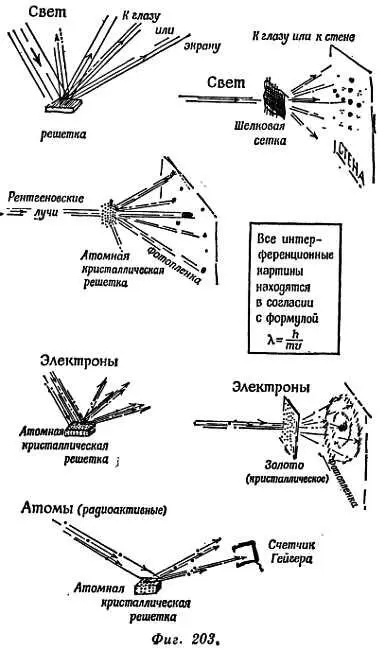
Идею дуализма «волна — частица» трудно воспринять для света, но еще труднее — для атомов, электронов и всех кусочков вещества. Свет, проходящий через пару щелей в стенке, образует на удаленном экране интерференционные полосы Юнга. Но его энергия, очевидно, переносится пулеподобными квантами, большая часть которых попадает на яркие и лишь малое число квантов — на темные полосы. Если через две щели проходит поток электронов [199], снова получается интерференционная картина, так что каждый индивидуальный электрон должен каким-то образом пройти через обе щели [200]. Его волна должна проходить через обе щели, иначе как же получится интерференционная картина? Но как это может сделать пуля?

Волновые пакеты

По отношению к этому парадоксу де-Бройль выдвинул некоторые утешительные соображения — но его аргументы сложны и требуют математики в большей мере, чем мы здесь дадим, Его идея состояла в следующем: представлять волны, соответствующие фотонам или частицам вещества, как компактную группу мелких волн, подобную всплеску на воде, который можно создать одиночным шлепком по поверхности воды в ванне или бассейне.

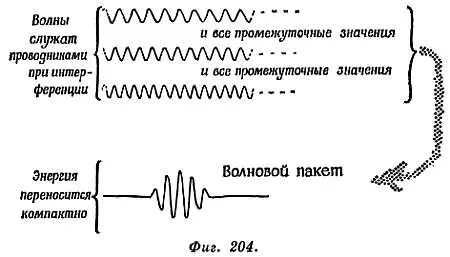
Проследите, как такая группа волн распространяется по воде; вы увидите, что она с определенной скоростью v расплывается как кольцо возмущения. Теперь понаблюдайте за деталями такой группы при ее распространении. Она содержит маленькие волны, перемещающиеся медленнее , чем вся группа в целом. Маленькие волны позади передовой группы непрерывно погибают, тогда как на фронте группы рождаются новые волны. Эта идея группы волн, обладающих различными скоростями, составляет суть схемы де-Бройля. Электроны и световые кванты (фотоны) представляют собой группы волн, компактно переносящие энергию и импульс.

То, что мы обычно наблюдаем как «частицу» (электрон, протон, фотон…), — это «волновой пакет» (см. фиг. 272 ч. I). Однако «всплески» внутри него образованы многими близкими длинами волн, которые собираются вместе, создавая результирующую картину. Эти наборы волн находятся в фазе вблизи центра группы, а переходя в другие места, они взаимно погашаются. Но каждую индивидуальную волну-составляющую можно рассматривать как простирающийся далеко вперед и назад «путепровод». Это волна, которая приводит частицу-пакет к светлой полоске в интерференционной картине. Волны, ведущие частицу, перемещаются быстрее, чем вся группа в целом, в противоположность волнам на воде. Импульс частицы с массой m и скоростью v равен mv ; ее волновой пакет перемещается с групповой скоростью v , волнам пакета соответствует длина волны h / mv . А сами волны перемещаются со скоростью V , большей v . В действительности V∙ v= c 2, так что V даже больше с . Это не противоречит теории относительности, поскольку V — только скорость перемещения фазы волны, а не скорость распространения энергии. Вы можете представить себе волны, которые бегут впереди частицы, чтобы разметить интерференционную картину и сообщить частице, куда ей следует идти. Загадка дуализма «волна-частица» при этом сохраняется, но все же легче совместить идею волны с частицей, если говорить, что «то, что вы обычно наблюдаете как частицу, представляет собой компактный пакет волн (волновой пакет)» (взгляните снова на фиг. 272 ч. I).

Идея де-Бройля не только объяснила эксперименты, в которых у электронов и других частиц обнаруживается волновое поведение, но и с совершенно неожиданной стороны осветила модель Бора. А затем привела к великому развитию современной атомной теории.

Волны и атом Бора

Де-Бройль прояснил причину загадочного правила mv∙2π r= nh, установленного Бором для разрешенных орбит. Описывающий такую орбиту электрон имеет длину волны λ= h/ mv, так что mv= h/ λ. Тогда правило Бора приводит к соотношению ( h/ λ)∙2π r= nh, или 2π r= nλ. С этой точки зрения стабильными являются только такие орбиты, на которых длина волны электрона укладывается целое число раз ( n ): 2π r 1= λ 1, 2π r 2= λ 2, 2π r 3= λ 3и т. д. Электрон должен, так сказать, вплетать свою волну туда, где она уже есть (подобно змее, глотающей свой собственный хвост), и образовывать стоячую волну (см. гл. 10 ) с целым числом длин волн на окружности [201](фиг. 206). Тогда мы уже видим не твердую частицу с центростремительным ускорением v 2/ r , которая должна была бы излучать, а волновую картину, заполняющую орбиту. Для многих физиков такая картина давала но крайней мере удобное объяснение произвольного правила Бора: «разрешенные орбиты» соответствуют допустимым стоячим волнам.

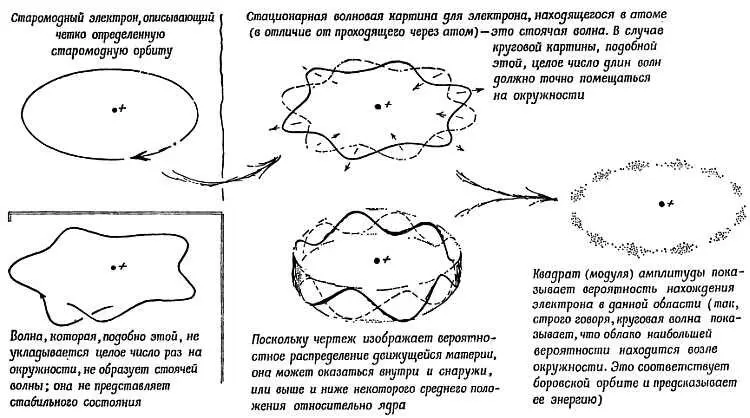
Фиг. 206. Модель атома Бора, в которой электроны заменены волнами де-Бройля.

Теперь мы рассматриваем эти волны де-Бройля как схему, которая сообщает нам о возможном местонахождении электрона: чем сильнее [202]волна в какой-либо области, тем вероятнее, что мы обнаружим там электрон. Эти волны — бегущие волны для движущихся свободных электронов или стоячие волны для электронов, связанных в атоме, — не есть волны движущегося вещества или переменного поля — это «волны вероятности». Кольцевые волны, предложенные впервые для объяснения боровских орбит, могут определять вероятность местонахождения электрона в некоторой области возле окружности. Либо они могут быть эквивалентны волнам, бегущим навстречу друг другу по кольцу. Тогда уже бесполезно спрашивать, в какой точке окружности расположен электрон. В настоящее время для указания вероятности местонахождения электрона мы имеем другие волновые картины для разных состояний: радиальные и круговые стоячие волны. Первая боровская орбита атома водорода заменена радиальной кривой, показывающей интенсивность волны и доходящей до самого ядра. Хотя большую часть времени электрон проводит на разных расстояниях от ядра, среднее расстояние совпадает с предсказанным ранее Бором. А если эту кривую симметрично покрутить по всем направлениям, она изобразит для электрона облако вероятности, рассеянное вокруг ядра. Волновые картины для более сложных атомов и для более высоких энергетических состояний показывают более сложную форму облака. Каждая картина изображает только облако вероятности местонахождения электрона, но частота волнового движения для данной картины является определенной, а это означает определенность уровня энергии электрона.