Дэйв Голдберг - Вселенная в зеркале заднего вида. Был ли Бог правшой? Или скрытая симметрия, антивещество и бозон Хиггса

Чем же так полезен подход Ферма при всей своей извилистости? В лучшем случае просто получишь тот же результат, что и при применении принципа Гюйгенса. Дело в том, что принцип Ферма придуман не для того, чтобы получить правильный ответ: он призван объяснить, что происходит на самом деле.

Принцип Ферма оказался на удивление полезен для современных открытий. Один из поразительных прогнозов, которые дала общая теория относительности, — время возле массивного тела, например, звезды или черной дыры, течет медленнее, чем вдали от него. Поскольку свет по-прежнему хочет пробежать по самому быстрому маршруту, он отклонится от прямой линии, чтобы объехать вызванные гравитацией пробки поблизости от черной дыры. Проще говоря, тот самый принцип, который предсказывает поведение призм, предсказывает и то, что массивные тела искривляют свет.

Часто бывает, что самый короткий путь — не прямой. Вот, например, вам нужно добраться из Филадельфии в Пекин. Какой маршрут выбрать? Если вам случалось летать трансокеанским рейсом и, чтобы не свихнуться от скуки, наблюдать за перемещением самолета по компьютерной карте, возможно, вы заметили, что самолет летит не по той линии, которая вам по наивности представлялась прямой. Пекин с Филадельфией находятся примерно на одной широте — около 40 градусов. И все же путь, по которому полетит ваш самолет, пройдет севернее Аляски.

Этот путь по большой дуге проделывает именно то, что предлагает Ферма. Это тот маршрут между Филадельфией и Пекином, который минимизирует дистанцию. Примерно то же самое у вас получится, если вы возьмете глобус, воткнете булавки в точки старта и финиша и туго-туго натянете между ними резинку. На карте большая дуга выглядит странно, однако это самый естественный маршрут в мире. Если вы полетите по прямой и нанесете свой маршрут на карту, как в кино про Индиану Джонса, путь по большой дуге получится сам собой.

Однако Ферма, как вы вскоре убедитесь, не просто подсказывает ближайший путь до Пекина — он еще и закладывает фундамент для формулирования всех физических законов, основанных на симметрии, а это возвращает нас прямиком к Эмми Нётер.

Принцип Ферма очень хорош и правилен, если нас интересует исключительно распространение света, но если мы пытаемся разобраться в устройстве мироздания, придется копнуть поглубже. Принцип Ферма не объясняет создание частиц и античастиц, существование сил, полей, расширение вселенной и примерно миллион прочих явлений, наблюдаемых во вселенной, где мы живем.

У физиков и математиков — а в XVII веке разница между ними совсем не была колоссальной — подобные задачи на минимизацию нашли выражение в попытках найти новые интересные способы приложения только что открытых законов Ньютона. Одна из самых известных задач того времени — поиск кривой под названием «брахистохрона» [53] «Кратчайшее время» по-древнегречески, если вам интересно. И, что бы вы ни думали, к динозаврам это отношения не имеет. .

Представьте себе, что вы хотите построить самые-самые распрекрасные американские горки — ну чтобы уж точно все ахнули. Вы можете предельно минимизировать силу трения, но при попытках построить идеальную форму непременно наткнетесь на маленькую математическую тайну. Проектировать американские горки надо так, чтобы вагонетка, стартующая из состояния покоя в точке А, как можно быстрее очутилась внизу, в точке В.

Загадка брахистохроны не теряла актуальности некоторое время, а потом, в 1696 году, Иоганн Бернулли — представитель очень знаменитой семьи, где было много выдающихся математиков — заявил, что решил задачу, и не без самодовольства поставил ее перед другими математиками: потягайтесь, мол, со мной.

Я, Иоганн Бернулли, обращаюсь к самым блестящим математикам в мире. Для умного человека нет ничего привлекательнее честной и трудной задачи, возможное решение которой стяжает им славу и останется в веках… Если кто-то сообщит мне решение представленной задачи, я публично объявлю, что он достоин похвалы [54] Даже мне хочется пнуть этого индюка! .

Сам Бернулли придумал очень хитроумное решение задачи, так что похвалялся он, наверное, не зря. Вагонетка американских горок едет чем ближе к земле, тем быстрее — а Бернулли представил себе очень сложную линзу, материал которой чем выше, тем плотнее, так что свет, проходя сквозь нее сверху вниз, будет бежать чем ближе к земле, тем быстрее. Потом Бернулли применил принцип Ферма — и потребовал, чтобы луч прошел заданное расстояние за минимальное время.

Полученная кривая получила название перевернутой циклоиды и очень похожа на обычную миску, только очень точную, математически выведенную.

Все это стало возможным в основном благодаря тому, что лет за десять до этого Исаак Ньютон опубликовал свой трактат « Principia Mathematica ». К тому времени, как Бернулли опубликовал свой вызов, Ньютон уже работал управляющим Королевского монетного двора, однако же нашел время подумать над задачей о брахистохроне. Решил он ее за один вечер перед сном — совсем иначе, чем Бернулли, геометрическим методом. Был он таким математическим врединой, что даже не стал подписываться. Но Бернулли все равно понял, кто это, отметив: «По когтю опознаю льва».

Находить форму кривых в XVII веке было очень модно. Другая знаменитая задача касалась поиска кривой с названием «таутохрона» [55] По-древнегречески буквально «то же время». . Если сделать американские горки такой формы, то откуда бы вы ни пустили вагонетку, она доберется до низу за одно и то же время. Эту задачу решил в 1659 году Христиан Гюйгенс — тот самый, что описал свет как волну. Почему это такое большое достижение, становится понятно, если учесть, что до публикации « Principia Mathematica » оставалось еще почти 30 лет.

Циклоида

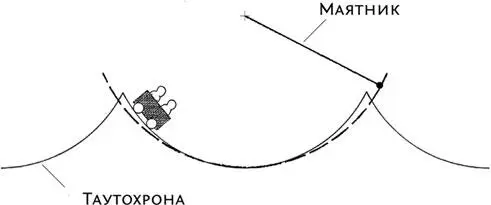
Я заговорил о таутохроне, поскольку выясняется, что она представляет собой точно такую же кривую, что и брахистохрона — циклоиду. Помимо того, что таутохрона — ответ на математическую задачу, она приносит много пользы, поскольку на тех же принципах можно построить и точные часы. На протяжении почти всей мировой истории единственными точными часами на свете было Солнце, а поскольку XVII век был периодом географических открытий и мореплавания, солнечные часы, конечно, уже не годились.

Обратите внимание, что в самом низу таутохрона очень похожа на кривую, которую описывает маятник. И не случайно. Маятники потому и позволяют часам так точно отмерять время, что при условии, что отклонение будет относительно малым, колебания занимают в точности одно и то же время — вот почему дуга маятника так хорошо вписывается в донышко циклоиды. Галилей еще в юности отметил этот факт экспериментально. Ему было скучно, он наблюдал за колебаниями люстры в соборе в Пизе и отметил, что размах колебаний уменьшается, однако время (в ударах сердца) остается постоянным.