Роджер Пенроуз - Новый ум короля: О компьютерах, мышлении и законах физики

Я сначала напомню вам используемую в квантовой механике так называемую процедуру редукции вектора состояния ( R) (см. рис. 6.23). Рис. 8.1 иллюстрирует (условно) характер предполагаемой эволюции вектора состояния | ψ ) в квантовой механике.

Рис. 8.1.Временная эволюция вектора состояния: гладкая унитарная эволюция U (в соответствии с уравнением Шредингера), перемежаемая с разрывной редукцией R вектора состояния

Как видим, этот характер довольно своеобразный: считается, что бо́льшую часть времени эволюция происходит в соответствии с унитарной эволюционной процедурой U(уравнение Шредингера), но в некоторые моменты времени, когда предполагается, что происходит «наблюдение» (или «измерение»), применяется R- процедура и вектор состояния скачком переходит в другой вектор состояния, | X ), где | X ) представляет собой одну из двух или нескольких ортогональных альтернативных возможностей | X ), | ψ ), | θ )…, определяемых природой конкретного производимого наблюдения О. Тогда вероятность р скачкообразного перехода от | ψ ) к | X ) определяется уменьшением квадрата длины | ψ ) 2 вектора | ψ ) при проекции | ψ ) (в гильбертовом пространстве) на направление вектора | X ) (Математически это равно величине уменьшения | X ) 2 при проекции вектора | X ) на направление | ψ ).) В таком виде эта процедура оказывается асимметричной во времени, поскольку сразу же после выполнения наблюдения Овектор состояния должен принадлежать к заданному множеству | X ), | ψ ), | θ )…, возможных значений, определяемых О, в то время как непосредственно перед наблюдением Овектор состояния должен был иметь значение | ψ ), которое не обязано быть равным ни одному из элементов упомянутого множества. Однако, это всего лишь кажущаяся асимметричность и она может быть устранена, если посмотреть на эволюцию вектора состояния с другой точки зрения. Рассмотрим квантово-механическое решение, обращенное во времени . Это экстравагантное описание проиллюстрировано на рис. 8.2.

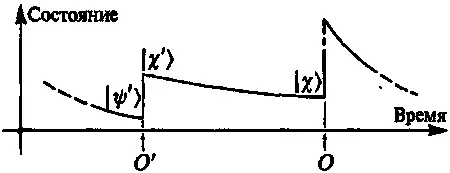
Рис. 8.2.Более экстравагантное изображение эволюции вектора состояния, описанное вспять по времени. Расчетная вероятность, связывающая наблюдение в точке О с наблюдением в точке О', такая же, как и в случае, изображенном на рис. 8.1, но к чему относится это вычисленное значение?

Мы предполагаем, что вектор состояния равен | X ) непосредственно перед О, а не сразу после этого наблюдения, и применим процедуру унитарной эволюции вспять по времени вплоть до момента предыдущег о наблюдения О ' . Предположим, что в результате обратной эволюции мы получим состояние, описываемое вектором | X' ) (сразу же после наблюдения О ' ). В нормальном описании эволюции вперед во времени, изображенном на рис. 8.1, сразу же вслед за О ' мы имели другое состояние | ψ' ) (результат наблюдения О ' , при котором эволюция вперед во времени вектора | ψ' ) переводит его в | ψ ) в момент наблюдения О). Теперь в нашем обращенном во времени описании у вектора | ψ' ) тоже есть своя роль: он представляет состояние системы непосредственно перед О ' . Вектор состояния | ψ' ) соответствует состоянию, фактически наблюдавшемуся в точке О ' , так что с «обращенной» точки зрения мы рассматриваем | ψ' ) как результат наблюдения О ' в обращенном вспять времени . Расчетное значение квантовомеханической вероятности р' , связывающее результаты наблюдений в точках Ои О ' , теперь определяется уменьшением величины | X'| 2 при проекции | X' ) в направлении | ψ' ) (что равно уменьшению | ψ'| 2при проекции | ψ' ) в направлении | ψ' )). То, что мы получим то же самое значение, что и раньше, является фундаментальным свойством оператора U [193].

Таким образом, может создаться видимость установления симметричности во времени квантовой теории даже в случае, когда помимо обычной процедуры унитарной эволюции Uучитывается также и разрывный процесс, описываемый процедурой редукции Rвектора состояния. Это, однако, неверно . Квантовая вероятность р описывает — независимо от того, как она рассчитывается — вероятность получить результат (а именно, | X )) в точке Опри условии определенного результата (а именно, | ψ' )) в точке О ' . Эта вероятность не обязательно равна вероятности получить данный результат в точке О ' при условии данного результата в точке О, а ведь именно последнюю вероятность [194]и должна определить обращенная во времени квантовая механика. Просто удивительно, до чего много физиков молчаливо полагают эти две вероятности равными друг другу. (Я сам этим грешил — см. Пенроуз [1979б], с. 584.) Однако наиболее вероятно, что эти две вероятности совершенно различны и только первая из них правильно определяется в рамках квантовой механики!

Давайте поясним эту ситуацию на простом конкретном примере. Предположим, что у нас есть лампа L и фотоэлемент (то есть, детектор фотонов) Р . Между L и P разместим полупосеребренное зеркало М, наклонив его под углом равным, скажем, 45 ° к линии, соединяющей точки L и Р (рис. 8.3).

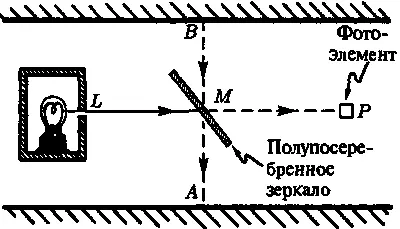
Рис. 8.3.Необратимость во времени R- процедуры в простом квантовом эксперименте. Вероятность регистрации фотона фотоэлементом при условии излучения фотона источником равна в точности одной второй, но вероятность излучения фотона источником при условии , что фотоэлемент зарегистрировал фотон, заведомо не равна одной второй

Предположим, что лампа время от времени случайным образом испускает фотоны, и что конструкция ее такова (в ней используются параболические зеркала), что фотоны всегда оказываются очень точно нацеленными на Р . При каждом попадании фотона на фотоэлемент последний регистрирует это событие, причем мы предполагаем, что устройство срабатывает со 100 %-ной надежностью. Предположим также, что каждый факт излучения фотона регистрируется в точке L и тоже со 100 %-ной надежностью. (Ни одно из этих идеализированных требований не противоречит принципам квантовой механики, хотя практическое достижение такой эффективности может представлять определенные трудности.)