Роджер Пенроуз - Новый ум короля: О компьютерах, мышлении и законах физики

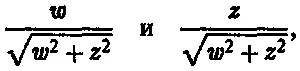
которые лежат внутри единичной окружности.

Теперь мы видим, что амплитуда вероятности в конечном счете представляет собой аналог не настоящей вероятности, а скорее «комплексного квадратного корня» из вероятности. Что происходит с ней, когда эффекты квантового уровня увеличиваются настолько, что достигают классического уровня? Напомним, что, манипулируя с вероятностями и амплитудами, мы иногда сталкивались с необходимостью производить их умножение и сложение. Прежде всего заметим, что операция умножения не сопряжена с какими-либо проблемами при переходе от квантовых правил к классическим. Происходит это вследствие замечательного математического факта: квадрат модуля произведения двух комплексных чисел равен произведению квадратов модулей каждого из чисел:

| zω | 2 = | z | 2 | ω | 2 .

(Это свойство непосредственно следует из геометрического смысла произведения двух комплексных чисел, приведенного в главе 3, но на языке действительной и мнимой частей z = х + iу , ω = u + iv ; это — прекрасное маленькое чудо. Проверьте сами!)

Из этого факта следует, что если в эксперименте с двумя щелями для частицы существует только один маршрут (открыта только одна щель, например t ), то рассуждения можно строить «классически», и вероятности получатся одними и теми же, независимо от того, наблюдаем ли мы за прохождением частицы в промежуточных точках ее пути (в щели t ) [142]. А квадраты модулей можно будет взять на любой стадии наших вычислений, например,

| A ( s , t )| 2 х | A ( t , p )| 2 = | A ( s , t ) х A ( t , p )| 2 .

Ответ — результирующая вероятность — получится одним и тем же.

Но если перед частицей открыт более чем один маршрут (например, если открыты обе щели), то необходимо образовывать сумму , и здесь-то и начинают обнаруживаться характерные особенности квантовой механики. Когда мы образуем квадрат модуля суммы ω + z двух комплексных чисел ω и z , мы обычно не получаем только лишь сумму квадратов модулей этих чисел; существует дополнительный «поправочный член»:

| ω + z | 2 = | ω | 2 + | z | 2 + 2 | ω || z | cosθ ,

где θ — угол, образуемый направлениями на точки z и ω из начала координат на плоскости Аргана (рис. 6.9).

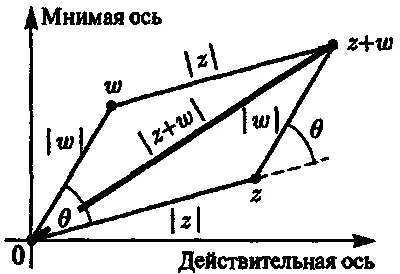
(Напомним, что косинус угла есть отношение «прилежащий к углу катет/гипотенуза» для прямоугольного треугольника. Пытливый читатель, незнакомый с этой формулой, может попытаться самостоятельно вывести ее, используя геометрию, изложенную в главе 3. В сущности эта формула есть не что иное, как слегка «замаскированное» хорошо известное «правило косинуса»!) Именно поправочный член 2 | ω || z | cosθ описывает квантовую интерференцию между квантовомеханическими альтернативами. Значение cosθ заключено между -1 и 1 . При θ = 0 ° мы имеем cosθ = 1 , и две альтернативы усиливают друг друга так, что полная вероятность оказывается больше суммы отдельных вероятностей. При θ = 180 ° мы имеем cosθ = - 1 , и две альтернативы стремятся погасить друг друга, в результате чего полная вероятность оказывается меньше суммы отдельных вероятностей (деструктивная интерференция). При θ = 90 ° мы имеем cosθ = 0 , и получается ситуация, промежуточная между двумя упомянутыми выше: две вероятности просто суммируются. Для больших или сложных систем поправочные члены обычно «усредняются», так как «среднее» значение cosθ равно нулю, и мы получаем обычные правила классической вероятности! Но на квантовом уровне эти члены описывают важные интерференционные эффекты.

Рассмотрим эксперимент с двумя щелями, когда обе щели открыты. Амплитуда того, что фотон достигает точки р , равна сумме ω + z , где

ω = A ( s , t ) x A ( t , p ) и z = A ( s , b ) x A ( b , p ).

В самых ярких точках экрана имеем: ω = z (так что cosθ = 1 ), откуда

| ω + z | 2 = | 2ω | 2= 4 | ω | 2 ,

что в 4 раза больше вероятности | ω | 2 , когда открыта только верхняя щель, и приводит к увеличению интенсивности потока большого числа фотонов в 4 раза, в полном согласии с экспериментом. В темных точках экрана имеем ω = — z (так что cosθ = - 1 ), откуда

| ω + z | 2= | ω — ω | 2= 0 ,

т. е. интенсивность равна нулю (деструктивная интерференция!) также в соответствии с наблюдением. Точно посередине между этими точками мы имеем: ω = iz или ω = — iz (так что cosθ = 0 ), откуда

| ω + z | 2 — | ω ± iω | 2 = | ω | 2 + | ω | 2 = 2 | ω | 2 ,

что дает вдвое бо́льшую интенсивность освещенности по сравнению с освещенностью только при одной щели (как в случае с классическими частицами). В конце следующего раздела мы узнаем, как рассчитывать, где именно расположены яркие, темные точки и точки с промежуточной интенсивностью освещенности.

И в заключение одно замечание. Когда открыты обе щели, амплитуда того, что частица достигнет точки р через щель t , в самом деле равна ω = A ( s , t ) х A ( t , p ), но мы не можем интерпретировать квадрат ее модуля | ω | 2 как вероятность того, что частица «действительно» прошла через верхнюю щель, чтобы достигнуть точки р . Такая интерпретация привела бы нас к бессмысленным ответам, в особенности, если точка р находится в темном месте на экране. Но если мы захотим «зарегистрировать» присутствие фотона в щели t , то усиливая эффект его присутствия (или отсутствия) там до классического уровня, мы можем использовать величину | A ( s , t )| 2 в качестве вероятности того, что фотон действительно присутствует в щели t . Но такое наблюдение нарушило бы картину распределения волн. Для того, чтобы произошла интерференция, нам необходимо убедиться в том, что прохождение фотона через щели остается на квантовом уровне , так чтобы оба альтернативных маршрута давали свой вклад и иногда могли гасить друг друга. На квантовом уровне отдельные альтернативные маршруты обладают только амплитудами, но не вероятностями.