Майкл Файер - Абсолютный минимум. Как квантовая теория объясняет наш мир

Рис. 13.7. Диаграмма энергетических уровней МО для гипотетической молекулы Ne 2 . Два атома неона обладают двадцатью электронами. Получается одинаковое число связывающих и разрыхляющих электронов, так что связи не образуется. Молекулы Ne 2 не существует

Молекула O 2— это первый пример, в котором правило Хунда вступает в действие и играет важную роль. Обратите внимание: при заполнении энергетических уровней электронами два последних электрона имеют неспаренные спины. Возможность иметь неспаренные спины без нарушения принципа Паули появляется благодаря тому, что существует две разных разрыхляющих π-МО. Орбиталь π x *возникает за счёт бокового перекрытия двух атомных p x-орбиталей (см. рис. 13.3), а орбиталь π y *появляется за счёт бокового перекрытия двух атомных p y-орбиталей. Правило Хунда утверждает, что электроны будут занимать орбитали без спаривания, если это не противоречит принципу Паули и не требует подъёма на значительно более высокоэнергетическую орбиталь. Две обсуждаемые разрыхляющие МО имеют одинаковую энергию, так что правило Хунда вступает в игру.

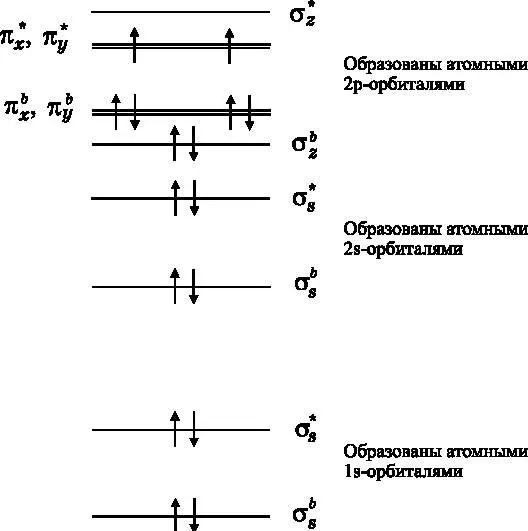
Рис. 13.8. Диаграмма энергетических уровней МО для молекулы O 2 . Имеются одна пара σ -связывающих электронов и одна пара π -связывающих электронов. Молекула O 2 имеет двойную связь. Обратите внимание на неспаренные электроны связывающей π -МО

Электрон обладает магнитным моментом. В некотором смысле он действует как крохотный магнитный брусок. У него есть северный и южный полюса. Термин «спин» {20} 20 От англ. spin — вращение, вращаться. — Примеч. пер. для квантового числа электрона пришёл из классической механики. В классической теории вращающийся пространственно распределённый заряд обладает магнитным моментом. Электрон — это волна амплитуды вероятности. Он имеет делокализованное распределение заряда. В результате у него есть магнитный момент, но этот факт не следует понимать как вращение в буквальном смысле. Это классическая идея. Дирак, которому мы обязаны концепцией абсолютного размера (см. главу 2), объединив квантовую теорию с теорией относительности Эйнштейна, показал, почему электрон обладает магнитным моментом. Электрон в действительности не вращается, но это название закрепилось. Магнитный момент электрона играет важную роль.

Когда спины двух электронов спарены, северный полюс одного крошечного магнита совпадает по направлению с южным полюсом другого. Магнитные свойства одного электрона компенсируют магнитные свойства другого. Однако в молекуле O 2два электрона не спарены. Их спины имеют одинаковое направление. В результате молекула O 2приобретает свойство, называемое парамагнетизмом. Она реагирует на магнит. Вода при температуре выше 100 °C находится в газообразном состоянии, но если охладить её до температуры ниже 100 °C, она превращается в жидкость. С кислородом происходит то же самое, но его требуется охлаждать гораздо сильнее. При комнатной температуре кислород является газом, но если очень сильно его охладить (ниже −183 °C), он переходит в жидкое состояние. Можно налить жидкий кислород в пробирку, подвешенную на нити. Если поднести к этой пробирке магнит, то он её притянет. Спины электронов (маленькие магнитные бруски) в молекулах O 2выстраиваются вдоль магнитного поля внешнего макроскопического магнита. Эти выстроившиеся крошечные магнитики, складываясь вместе, придают жидкому кислороду магнитные свойства, и пробирка притягивается к внешнему магниту.

Корректное предсказание парамагнитных свойств O 2, сделанное на основе анализа диаграммы энергетических уровней МО, — это замечательный результат. Магнитный момент O 2— это сугубо квантовый эффект, и наше предсказание того, что O 2является парамагнетиком, появилось благодаря применению правила Хунда. Следуя определённым правилам, мы нарисовали линии, отвечающие энергетическим уровням. Затем, следуя другим правилам, мы разместили на этих линиях энергетических уровней стрелки, направленные вверх и вниз (расселили по ним электроны). На основе этих линий и стрелок мы смогли предсказать, что молекула кислорода является магнитной, хотя молекулы фтора и азота таковыми не являются.

На рис. 13.9 представлена заполненная диаграмма энергетических уровней МО для азота N 2. Атом азота находится в Периодической таблице непосредственно слева от кислорода. Обратите внимание, что есть перестановка в порядке следования связывающих МО, порождённых p -электронами. Подробные квантовомеханические вычисления позволяют получить порядок следования и значения энергетических уровней МО. У азота этот порядок иной, чем у O 2и F 2. Атом азота имеет семь электронов, так что молекула N 2содержит 14 электронов. Как и в случае с F 2и O 2, 1 s - и 2 s -электроны не участвуют в связывании, поскольку они заполняют как связывающие, так и разрыхляющие МО. На заполнение этих МО уходит восемь из 14 электронов. Остальные шесть электронов расселяются по трём связывающим МО — одной σ-МО и двум π-МО. На разрыхляющих π-МО и σ-МО, образованных p z-орбиталями, электронов нет. Таким образом, N 2имеет связь порядка 3, то есть тройную связь. Тройная связь сильнее и короче, чем двойная или одиночная. Обратите внимание, что в молекуле N 2нет неспаренных электронов. Она не является парамагнитной. При низкой температуре (ниже −196 °C) азот становится жидким. Однако сдвинуть пробирку с жидким азотом с помощью магнита не получится, поскольку у него нет неспаренных спинов.

В главе 11, обсуждая связывание на основе положения атома в Периодической таблице, мы воспользовались представлением о том, что атом стремится сформировать ковалентные связи таким образом, чтобы совместное использование электронов позволяло ему достичь конфигурации благородного газа. Для обсуждаемых здесь элементов второй строки Периодической таблицы — азота, кислорода и фтора — таким благородным газом является неон. Как уже говорилось, атом фтора, который на один электрон отстаёт от конфигурации атома неона, будет совместно с другим атомом использовать один электрон. Атом кислорода, на два элемента отстающий от конфигурации атома неона, будет использовать два электрона, а атом азота, которому до неона не хватает трёх электронов, будет совместно использовать три электрона.

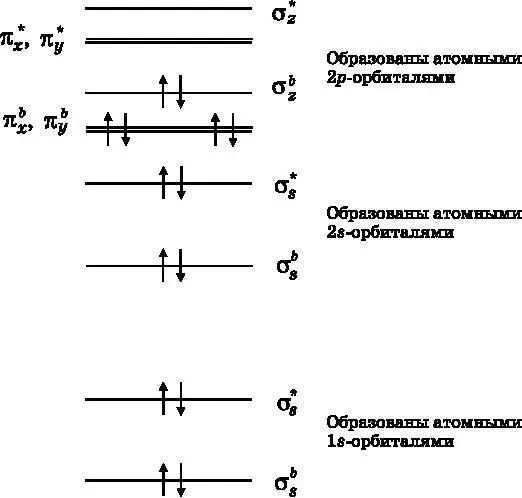
Рис. 13.9. Диаграмма энергетических уровней МО для молекулы N 2. Имеется одна дополнительная пара σ -связывающих электронов и две дополнительные пары π -связывающих электронов. N 2 имеет тройную связь