Ричард Фейнман - 8a. Квантовая механика I

Дальше все уже совсем легко. У нас есть формулы для энер­гий. Нам нужен гамильтониан, линейный по В х , В y и B z , который даст именно такие энергии, если применить нашу общую фор­мулу (8.3). Задача — найти гамильтониан. Прежде всего за­метим, что энергия расщепляется симметрично и ее среднее значение есть нуль. Взглянув на (8.3), мы сразу же увидим, что для этого требуется

Н 22=- H 11.

(Заметьте, что это подтверждается тем, что нам уже известно при В x =В y =0; в этом случае Н 11 =-mB z и H 22=m B z .) Если теперь приравнять энергии из (8.3) к тому, что нам известно из (8.19), то получится

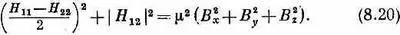
(Мы использовали также тот факт, что Н 21 =Н* 1 2 , так что H 12 H 21может быть записано в виде | Н 12 | 2.) Опять в частном случае поля в направлении z это даст

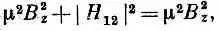
откуда | H 12| в этом частном случае равно нулю, что означает, что в H 12не может войти член с В z . (Вы помните, что мы гово­рили о линейности всех членов по В х , В y и B z .)

Итак, пока мы узнали, что в Н 11и H 22входят члены с В z , а в H 12и H 21— нет. Можно попробовать угадать формулы, которые будут удовлетворять уравнению (8.20), написав

H 11=-m В z,

H 22=m B z

и

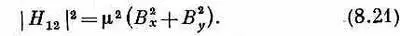
Оказывается, что никак иначе этого сделать нельзя!

«Погодите,— скажете вы,— H 12по В не линейно. Из (8.21) следует, что H 12=mЦ( В 2 x +В 2 y ) » . Не обязательно. Есть и дру­гая возможность, которая уже линейна, а именно

Н 12 =m ( В x +iB y ) .

На самом деле таких возможностей не одна, в общем случае можно написать

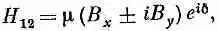
где d — произвольная фаза.

Какой же знак и какую фазу мы обязаны взять? Оказы­вается, что можно выбрать любой знак и фазу тоже любую, а физические результаты от этого не изменятся. Так что выбор — это вопрос соглашения. Еще до нас кто-то решил ставить знак минус и брать е i d=-1. Мы можем делать так же и написать

(Кстати, эти соглашения связаны и согласуются с тем про­изволом в выборе фаз, который мы использовали в гл. 4.) Полный гамильтониан для электрона в произвольном маг­нитном поле, следовательно, равен

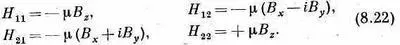
уравнения для амплитуд С 1и С 2таковы:

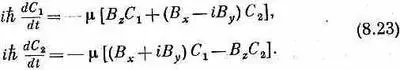
Итак, мы открыли «уравнения движения спиновых состояний» электрона в магнитном поле. Мы угадали их, пользуясь некото­рыми физическими аргументами, но истинная проверка всякого гамильтониана заключается в том, что он обязан давать предсказания, согласующиеся с экспериментом. Из всех сделанных проверок следует, что эти уравнения правильны. Более того, хотя все наши рассуждения относились к постоянному полю, написанный нами гамильтониан правилен и тогда, когда маг­нитные поля меняются со временем. Значит, мы теперь можем применять уравнения (8.23) для решения всевозможных инте­ресных задач.

§ 7. Вращающийся электрон в магнитном поле

Пример первый: пусть сначала имеется постоянное поле в направлении z. Ему соответствуют два стационарных состоя­ния с энергиями ±mB z . Добавим небольшое поле в направлении х. Тогда уравнения получатся такими же, как в нашей старой задаче о двух состояниях. Опять, в который раз, получается знакомый уже нам переброс, и уровни энергии немного расщеп­ляются. Пусть, далее, x -компонента поля начнет меняться во времени, скажем, как coswt. Тогда уравнения станут такими, как для молекулы аммиака в колеблющемся электрическом поле (см. гл. 7). И тем же способом, что и прежде, вы можете рассчитать процесс во всех деталях. При этом вы увидите, что колеблющееся поле приводит к переходам от +z-состояния к —z-состоянию и обратно, если только горизонтальное поле колеблется с частотой, близкой к резонансной, w 0=2m B z/ h . Это приводит к квантовомеханической теории явлений магнит­ного резонанса, описанной нами в гл. 35 (вып. 7).

Можно еще сделать мазер, в котором используется система со спином 1/ 2. Прибор Штерна — Герлаха создает пучок частиц, поляризованных, скажем, в направлении +z, и они потом направляются в полость, находящуюся в постоянном магнитном поле. Колеблющиеся в полости поля, взаимодействуя с магнит­ным моментом, вызовут переходы, которые будут снабжать полость энергией.

Рассмотрим теперь второй пример. Пусть у нас имеется магнитное поле В, направление которого характеризуется полярным углом 6 и азимутальным углом j (фиг. 8.10).

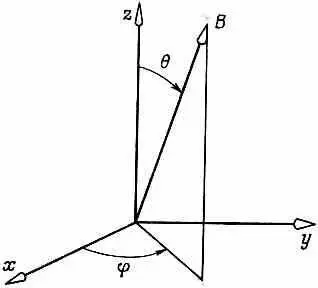
Фиг. 8.10. Направление В опре­деляется полярным углом q и ази­мутальным углом j.

Допу­стим еще, что имеется электрон, спин которого направлен по полю. Чему равны амплитуды С 1и С 2для этого электрона? Иными словами, обозначая состояние электрона |y>, мы хотим написать

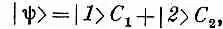
где C 1и С 2равны

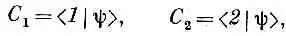
а | 1 > и | 2 >обозначают то же самое, что раньше обозначалось |+> и |-> (по отношению к выбранной нами оси z).

Ответ на этот вопрос также содержится в наших общих уравнениях для систем с двумя состояниями. Во-первых, мы знаем, что раз спин электрона параллелен В, то электрон нахо­дится в стационарном состоянии с энергией Е I =-mB. Поэтому и c 1и С 2должны изменяться как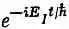

[см. уравнение (7.18)]; и их коэффициенты а 1и а 2даются формулой (8.5):