Ричард Фейнман - 8a. Квантовая механика I
- Название:8a. Квантовая механика I
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 8a. Квантовая механика I краткое содержание
8a. Квантовая механика I - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
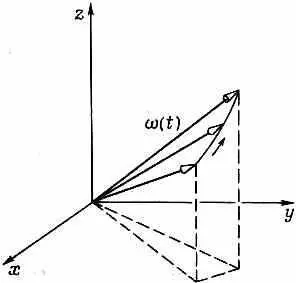
Фиг. 8.11. Направление спина электрона в изменяющемся магнитном поле В (t) прецессирует с частoтой w(t) вокруг оси, параллельной В.
Если все время это делать, вы остановитесь на какой-то конечной, ориентации спиновой оси, и амплитуды С 1и С 2получатся просто как ее проекции [при помощи (8.30)] на вашу систему координат.
Вы видите, что задача эта чисто геометрическая: надо заметить, где закончились все ваши вращения. Хотя сразу видно, что для этого требуется, но эту геометрическую задачу (отыскание окончательного итога вращений с переменным вектором угловой скорости) нелегко в общем случае решить явно. Во всяком случае, мы в принципе видим общее решение любой задачи для двух состояний. В следующей главе мы глубже исследуем математическую технику обращения с частицами спина 1/ 2и, следовательно, обращения с системами, обладающими двумя состояниями, в общем случае.
* Мы принимаем энергию покоя m 0 c 2 за «нуль» энергии и считаем магнитный момент m электрона отрицательным числом, поскольку он направлен против спина.
* Сказанное нами может вас слегка ввести в заблуждение. Поглощение ультрафиолетового света в принятой нами для бензола системе с двумя состояниями было бы очень слабым, потому что матричный элемент дипольного момента между двумя состояниями равен нулю. [Оба состояния электрически симметричны, и в нашей формуле (7.55) для вероятности перехода дипольный момент m равен нулю, и свет не поглощается.] Если бы других состояний не было, существование верхнего состояния пришлось бы доказывать иными путями. Однако более полная теория бензола, которая исходит из большего числа базисных состояний (обладающих, скажем, смежными двойными связями), показывает, что истинные стационарные состояния бензола слегка искажены по сравнению с найденными нами. В результате все же возникает дипольный момент, который и разрешает упомянутые в тексте переходы, приводящие к поглощению ультрафиолетового света.
* Мы немного упрощаем дело. Первоначально химики думали, что должны существовать четыре формы дибромбензола: две формы с атомами брома при соседних атомах углерода (орто-дибромбензол), третья форма с атомами брома при атомах углерода, идущих через один (.мета-дибромбензол), и четвертая форма с атомами брома, стоящими друг против друга (пара-дибромбензол). Однако отыскали они только три формы — существует лишь одна форма орто-молекулы.
* До тех пор, пока нет сильных магнитных полей, это предположение вполне удовлетворительно. Влияние магнитных полей на электрон мы обсудим в этой же главе позже, а очень слабые спиновые эффекты в атоме водорода — в гл. 10.
Глава 9
ЕЩЕ СИСТЕМЫ С ДВУМЯ СОСТОЯНИЯМИ
§ 1. Спиновые матрицы Паули
§ 2.Спиновые матрицы как операторы
§ З. Решение уравнений для двух состояний
§ 4. Состояния поляризации фотона
§ 5. Нейтральный K-мезон*
§ 6. Обобщение на системы с N состояниями
Повторить: гл. 33 (вып. 3) «Поляризация»
§ 1. Спиновые матрицы. Паули
Продолжаем обсуждение свойств двухуровневых систем. В конце предыдущей главы мы говорили о частице со спином l/ 2в магнитном поле. Мы описывали спиновое состояние, задавая амплитуду С 1того, что z-компонента спинового момента количества движения равна +h/2, и амплитуду С 2того, что она равна - h /2. В предыдущих главах мы эти базисные состояния обозначали |+> и |->. Прибегнем опять к этим обозначениям, хотя, когда это будет удобнее, мы будем менять их на | 1 > и | 2 >. Мы видели в последней главе, что когда частица со спином 1/ 2и с магнитным моментом m, находится в магнитном поле В =(В x , В y , B z ), то амплитуды С + ( =C 1)и С - (= С 2) связаны следующими дифференциальными уравнениями:
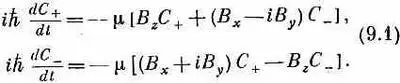
Иначе говоря, матрица-гамильтониан H ij имеет вид
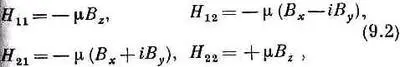
конечно, уравнения (9.1) совпадают с
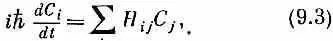
где i и j принимают значения + и - (или 1 и 2).
Эта система с двумя состояниями — спин электрона — настолько важна, что очень полезно было бы найти для ее описания способ поаккуратнее и поизящнее. Мы сейчас сделаем небольшое математическое отступление, чтобы показать вам, как обычно пишутся уравнения системы с двумя состояниями. Это делается так: во-первых, заметьте, что каждый член гамильтониана пропорционален m, и некоторой компоненте В; поэтому (чисто формально) можно написать
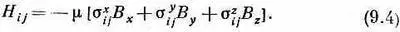
Здесь нет какой-либо новой физики; эти уравнения просто означают, что коэффициенты 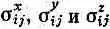 — их всего 4X3=12 — могут быть представлены так, что (9.4) совпадет с (9.2).
— их всего 4X3=12 — могут быть представлены так, что (9.4) совпадет с (9.2).
Посмотрим, почему это так. Начнем с B z . Раз В zвстречается только в H 11и H 22, то все будет в порядке, если взять

Мы часто пишем матрицу H ij в виде таблички такого рода:
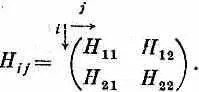
Для гамильтониана частицы со спином 1/ 2в магнитном поле В—это все равно что 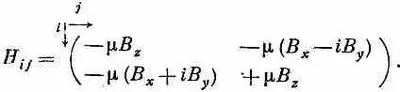
Точно так же и коэффициенты 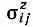 можно записать в виде матрицы
можно записать в виде матрицы
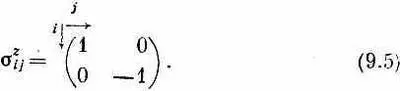
Расписывая коэффициенты при В х , получаем, что элементы матрицы s х должны иметь вид
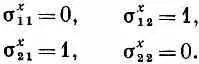
Интервал:
Закладка:






![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/1082376/pol-halpern-kvantovyj-labirint-kak-richard-fejnman.webp)

