Ричард Фейнман - 8a. Квантовая механика I
- Название:8a. Квантовая механика I
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 8a. Квантовая механика I краткое содержание
8a. Квантовая механика I - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
С матрицами о связан еще один очень интересный и важный момент. Можно, если угодно, представить себе, что три матрицы s х ., s y и s z подобны трем компонентам вектора; его иногда именуют «вектором сигма» и обозначают а. Это на самом деле «матричный вектор», или «векторная матрица». Это три разные матрицы, связанные каждая со своей осью х, у или z. С их помощью гамильтониан системы можно записать в красивом виде, пригодном для любой системы координат:

Таблица 9.2 · ПРОИЗВЕДЕНИЯ СПИНОВЫХ МАТРИЦ
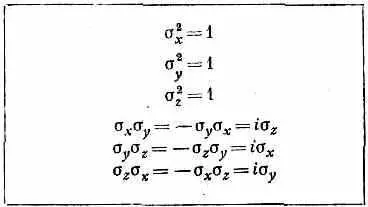
Хотя мы записали эти три матрицы в представлении, в котором понятия «вверх» и «вниз» относятся к направлению z (так что s zвыглядит особенно просто), но можно представить себе, как будут они выглядеть в любом другом представлении. И хотя это требует немалых выкладок, можно все же показать, что они изменяются как компоненты вектора. (Мы, впрочем, пока не будем заботиться о том, чтобы доказать это. Проверьте сами, если хотите.) Вы можете пользоваться о в различных системах координат, как если бы это был вектор.
Вы помните, что гамильтониан Н связан в квантовой механике с энергией. Он действительно в точности совпадает с энергией в том простом случае, когда состояний только одно. Даже в системе с двумя состояниями, какой является спин электрона, если записать гамильтониан в виде (9.13), он очень напоминает классическую формулу энергии магнита с магнитным моментом m в магнитном поле В. Классически это выглядит так:

где m — свойство объекта, а В — внешнее поле. Можно вообразить себе, что (9.14) обращается в (9.13), если классическую энергию заменяют гамильтонианом, а классическое m — матрицей (ms. Тогда после такой чисто формальной замены результат можно будет интерпретировать как матричное уравнение. Иногда утверждают, что каждой величине в классической физике соответствует в квантовой механике матрица. На самом деле правильнее было бы говорить, что матрица Гамильтона соответствует энергии и что у каждой величины, которая может быть определена через энергию, есть соответствующая матрица. Например, магнитный момент можно определить через энергию, сказав, что энергия во внешнем поле Весть — m· B. Это определяет вектор магнитного момента m . Затем мы смотрим на формулу для гамильтониана реального (квантового) объекта в магнитном поле и пытаемся угадать, какие матрицы соответствуют тем или иным величинам в классической формуле. С помощью этого трюка иногда у некоторых классических величин появляются их квантовые двойники.
Если хотите, попробуйте разобраться в том, как, в каком смысле классический вектор равен матрице ms ; может быть, вы что-нибудь и откроете. Но не надо ломать над этим голову. Право же, не стоит: на самом-то деле они не равны. Квантовая механика — это совсем другой тип теории, другой тип представлений о мире. Иногда случается, что всплывают некоторые соответствия, но вряд ли они представляют собой нечто большее, нежели мнемонические средства — правила для запоминания.
Иначе говоря, вы запоминаете (9.14), когда учите классическую физику; затем если вы запомнили соответствие m®ms, то у вас есть повод вспомнить (9.13). Разумеется, природа знает квантовую механику, классическая же является всего лишь приближением, значит, нет ничего загадочного в том, что из-за классической механики выглядывают там и сям тени квантовомеханических законов, представляющих на самом деле их подоплеку. Восстановить реальный объект по тени прямым путем никак невозможно, но тень помогает нам вспомнить, как выглядел объект. Уравнение (9.13) — это истина, а уравнение (9.14) — ее тень. Мы сперва учим классическую механику и поэтому нам хочется выводить из нее квантовые формулы, но раз и навсегда установленной схемы для этого нет. Приходится каждый раз возвращаться обратно к реальному миру и открывать правильные квантовомеханические уравнения. И когда они оказываются похожими на что-то классическое, мы радуемся. Если эти предостережения покажутся вам надоедливыми, если, по-вашему, здесь изрекаются старые истины об отношении классической физики к квантовой, то прошу прощения: сработал условный рефлекс преподавателя, который привык втолковывать квантовую механику студентам, никогда прежде не слыхавшим о спиновых матрицах Паули. Мне всегда казалось, что они не теряют надежды, что квантовая механика как-то сможет быть выведена как логическое следствие классической механики, той самой, которую они старательно учили в прежние годы. (Может быть, они просто хотят обойтись без изучения чего-то нового.) Но, к счастью, вы выучили классическую формулу (9.14) всего несколько месяцев тому назад, да и то с оговорками, что она не совсем правильна, так что, может быть, вы не будете столь неохотно воспринимать необходимость рассматривать квантовую формулу (9.13) в качестве первичной истины.
§ 2. Спиновые матрицы как операторы
Раз уж мы занялись математическими обозначениями, то хотелось бы описать еще один способ записи, способ, часто употребляемый из-за своей краткости. Он прямо следует из обозначений, введенных в гл. 6. Если имеется система в состоянии |y|( t )>, изменяющемся во времени, то можно, как мы это делали в уравнении (6.31), написать амплитуду того, что система при t +D t оказалась бы в состоянии | i >:

Матричный элемент | U(t, t +D t ) | j > — это амплитуда того, что базисное состояние | j > превратится в базисное состояние | i > за время D t . Затем мы определяли Н ij при помощи

и показывали, что амплитуды C i ( t )=< i |y( t )> связаны дифференциальными уравнениями

Если амплитуды C i записать явно, то это же уравнение будет выглядеть по-иному:
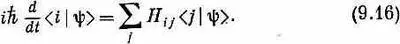
Интервал:
Закладка:






![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/1082376/pol-halpern-kvantovyj-labirint-kak-richard-fejnman.webp)

