Ричард Фейнман - 8a. Квантовая механика I

§ 4. Состояния поляризации фотона

Есть множество других интересных для изучения систем с двумя состояниями, и первая, о которой мы бы хотели пого­ворить,— это фотон. Чтобы описать фотон, нужно сначала задать вектор его импульса. У свободного фотона импульс определяет и частоту, так что указывать особо частоту не придется. Но еще остается одно свойство, именуемое поляризацией. Представьте себе фотон, приходящий к вам с определенной монохроматиче­ской частотой (которую во всем нашем обсуждении мы будем считать постоянной, так что можно не говорить о множестве состояний импульса).Тогда существуют два направления поля­ризации. По классической теории свет обладает, например, либо горизонтально колеблющимся электрическим полем, либо вертикально колеблющимся электрическим полем; этот свет двух сортов называют x -поляризованным и y -поляризованным светом. У света может быть и какое-то иное направление поляризации, его можно создать суперпозицией полей в направ­лении x и в направлении у. Или, взяв х- и y -компоненты со сдви­гом фаз в 90°, получить вращающееся электрическое поле — свет будет поляризован эллиптически. [Это краткое напомина­ние классической теории поляризованного света, которую мы изучали в гл. 33 (вып. 3).]

Пусть теперь у нас есть одиночный фотон, всего один. Уже нет электрического поля, которое можно было бы рассматривать прежним способом. Один-единственный фотон и ничего больше. по он тоже должен обладать аналогом классического явления поляризации. Значит, должны существовать по крайней мере два разных сорта фотонов. Сперва могло бы показаться, что их должно быть бесконечное множество, ведь, как бы то ни было, электрический вектор может быть направлен в любую сторону. Однако поляризацию фотона можно описать как систему с двумя состояниями. Фотон может быть либо в состоянии |х > , либо |в состоянии | у > . Под | х >подразумевается состояние поляризации каждого из фотонов в пучке света, который классически x -поляризован. А | у >означает состояние поляризации каждого из фотонов в y -поляризованном пучке. Эти | х >и |у >вы можете выбрать в качестве базисных состояний фотона с данным [направленным на вас импульсом—импульсом в направлении z.

Итак, существуют два базисных состояния | x > и | y >, и их вполне хватает, чтобы описать всякий фотон.

К примеру, если у нас есть поляроид, ось которого распо­ложена так, чтобы пропускать свет, поляризованный в направ­лении, которое мы называем направлением х, и если мы напра­вили туда фотон, который, как нам известно, находится в состоя­нии | у >, то он поглотится поляроидом. Если послать туда фотон, который, как нам известно, находится в состоянии | х > , он и выйдет в состоянии | x >. Когда мы берем кусок кальцита (исландского пшата), который расщепляет пучок поляризован­ного света на | x >-пучок и | y >-пучок, то этот кусок кальцита полностью аналогичен прибору Штерна — Герлаха, расщеп­ляющему пучок атомов серебра на два состояния |+> и |->. Значит, все, что мы раньше делали с частицами и приборами Штерна — Герлаха, можно повторить со светом и кусками поляроида. А что можно сказать о свете, который отфильтрован куском поляроида, повернутым на угол 6? Другое ли это состоя­ние? Да, действительно, это другое состояние. Обозначим ось поляроида х' , чтобы отличать ее от осей наших базисных состояний (фиг. 9.2).

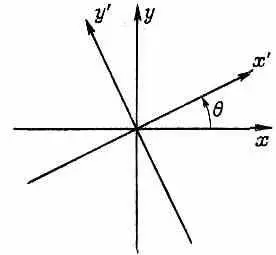
Фиг. 9.2. Оси координат, перпендику­лярные к вектору импульса фотона.

Выходящий наружу фотон будет в состоя­нии | х' >. Но всякое состояние может быть представлено в виде линейной комбинации базисных состояний, а формула для такой комбинации известна:

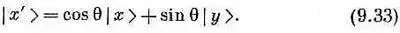
Иначе говоря, если фотон пройдет сквозь кусок поляроида, повернутого на угол q (по отношению к х), он все равно может быть разрешен на | x >- и | y >-пучки (например, куском каль­цита). Или, если угодно, вы можете в своем воображении просто разбить его на х- и y -компоненты. Любым путем вы получите амплитуду cosq быть в | х >-состоянии и амплитуду sinq быть в | y >-состоянии.

Теперь поставим такой вопрос: пусть фотон поляризован в направлении х' куском поляроида, повернутого на угол q,

и пусть он попадет в другой поляроид, повернутый на угол нуль (фиг. 9.3).

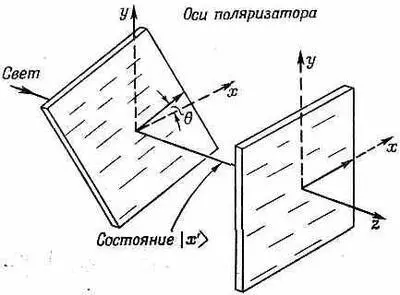
Фиг. 9.3. Две поляроидные пластины с углом q между плоскостями поляризации.

Что тогда произойдет? С какой вероятностью он прой­дет сквозь поляроид? Ответ: Пройдя первый поляроид, фотон наверняка оказывается в состоянии | х' > . Через второй поля­роид он протиснется лишь в том случае, если будет в состоянии | x > (и поглотится им, оказавшись в состоянии | у >). Значит, мы спрашиваем, с какой вероятностью фотон окажется в состоя­нии | x >? Эту вероятность мы получим из квадрата модуля амплитуды , амплитуды того, что фотон в состоянии | х' >находится также и в состоянии | x >. Чему равно < x | x '>? Умножив (9.33) на < x |, получим

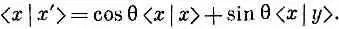
Но < x | y >=0; это следует из физики, так должно быть, если | х >и | у >суть базисные состояния, а < x | x >=l. И мы полу­чаем

< x | x '>=cosq,

а вероятность равна cos 2q. Например, если первый поляроид поставлен под углом 30°, то 3/ 4времени фотон будет проходить через него, a 1/ 4времени будет нагревать поляроид, поглощаясь внутри него.

Посмотрим теперь, что в такой же ситуации происходит с точки зрения классической физики. Там мы имели бы пучок света, электрическое поле которого меняется тем или иным обра­зом,— скажем «неполяризованный» пучок. После того как он прошел бы через первый поляроид, электрическое поле величи­ны x начало бы колебаться в направлении х' ; мы бы начертили его в виде колеблющегося вектора с пиковым значением x 0на диаграмме фиг, 9.4.

Фиг. 9.4. Классическая картина электрического вектора x.

Если бы затем свет достиг второго поля­роида, то черен него прошла бы только x -компонента x 0cosq электрического поля. Интенсивность была бы пропорциональна квадрату поля, т. е. x2cos 2q. Значит, проходящая сквозь последний поляроид энергия была бы в cos 2q слабее энергии, поступающей в него.