Ричард Фейнман - 8a. Квантовая механика I

И классическая, и квантовая картины приводят к одинако­вым результатам. Если бы вы бросили на второй поляроид 10 миллиардов фотонов, а средняя вероятность прохождения каждого из них была бы, скажем, 3/ 4, то следовало бы ожидать, что сквозь него пройдет 3/ 4от 10 миллиардов. Равным образом и энергия, которую они унесли бы, составила бы 3/ 4той энер­гии, которую вам хотелось протолкнуть через поляроид. Клас­сическая теория ничего не говорит о статистике этих вещей, она попросту утверждает, что энергия, которая пройдет на­сквозь, в точности равна 3/ 4той энергии, которая была пущена в поляроид. Это, конечно, немыслимо, если фотон только один. Не бывает 3/ 4фотона. Либо он весь здесь, либо его вовсе нет. И квантовая механика говорит нам, что он бывает весь здесь 3/ 4 времени. Связь обеих теорий ясна.

А как же с другими сортами поляризации? Скажем, с пра­вой круговой поляризацией? В классической теории компо­ненты х и у правой круговой поляризации были равны, но сдвинуты по фазе на 90°. В квантовой теории фотон, поляризо­ванный по кругу вправо («правый»), обладает равными ампли­тудами быть | х > - и | у >-поляризованным, и эти амплитуды сдвинуты по фазе на 90°. Обозначая состояние «правого» фотона через |II>, а состояние «левого» фотона через |Л>, можно написать [см. гл. 33, § 1 (вып. 3)]

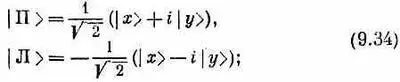
множитель 1/Ц2 поставлен, чтобы нормировать состояния. С помощью этих состояний можно подсчитывать любые эффекты, связанные с фильтрами или интерференцией, применяя законы квантовой теории. При желании можно также выбрать в каче­стве базисных состояний |П> и |Л> и все представлять через них. Надо только предварительно убедиться, что <���П|Л>=0, а это можно сделать, взяв сопряженный вид первого уравнения [см. (6.13)] и перемножив их друг с другом. Можно расклады­вать свет, пользуясь в качестве базиса и х-, и y -поляризациями, и х'-, и y' -поляризациями, а можно—и правой, и левой поляри­зациями.

Попробуйте (просто для упражнения) обратить наши фор­мулы. Можно ли представить состояние |х> в виде линейной комбинации правого и левого? Да, вот ответ:

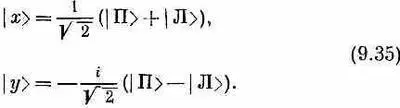
Доказательство: сложите и вычтите два уравнения в (9.34). От одного базиса к другому очень легко переходить.

Впрочем, одно замечание надо бы сделать. Если фотон поля­ризован по правому кругу, он не имеет никакого касательства к осям х и у. Если бы мы взглянули на него из системы коорди­нат, повернутой вокруг направления полета на какой-то угол, то свет по-прежнему был бы поляризован по кругу; то же с левой поляризацией. Право- и левополяризованный по кругу свет при любом таком повороте одинаков; определение не зависит от выбора направления х (если не считать того, что направление фотона задано). Великолепно, не так ли? Для определения не нужны никакие оси. Куда лучше, чем х и у !Но, с другой стороны, не чудо ли, что, складывая левое и правое, вы в состоянии узнать, где было направление x ? Если «правое» и «левое» никак не зависят от х, как же получается, что мы можем сложить их и вновь получить x ? На этот вопрос можно частью отве­тить, расписав состояние |П'>, представляющее фотон, правополяризованный в системе координат х', у'. В этой системе мы бы написали

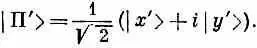
Как же будет выглядеть такое состояние в системе х, у? Подста­вим | х' > из (9.33) и соответствующее | у' >; мы его не выписывали, но оно равно (-sinq)| x >+(cosq)| y >. Тогда

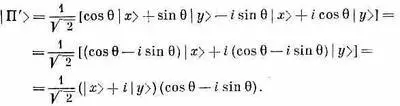
Первый множитель — это просто | П>, а второй е - i q ; итог таков:

Состояния | П'> и | П> отличаются только фазовым множи­телем е - i q . Если подсчитать такую же вещь для | Л' >, мы полу­чим

Теперь мы видим, что происходит. Сложив |П> и |Л>, мы получаем нечто отличное от того, что получилось бы при сложении |П'> и |Л'>. Скажем, x -поляризованный фотон есть [см. (9.35)] сумма |П> и |Л>, но y -поляризованный фо­тон — это сумма со сдвигом фазы первого на 90° назад, а вто­рого — на 90° вперед. Это просто то же самое, что получилось бы из суммы |П> и |Л'> при определенном выборе угла 0=90°, и это правильно, В штрихованной системе x -поляризация — это то же самое, что y -поляризация в первоначальной системе. Значит, не совсем верно, что поляризованный по кругу фотон выглядит в любой системе осей одинаково. Его фаза (фазовое соотношение между право- и левополяризованными по кругу состояниями) запоминает направление х.

§ 5. Нейтральный К-мезон**

Теперь мы расскажем о двухуровневой системе из мира странных частиц — о системе, для которой квантовая механика приводит к поразительнейшим предсказаниям. Полное описание этой системы потребовало бы от нас таких знаний о странных частицах, каких у нас пока нет, поэтому, к сожалению, кое- какие углы нам придется срезать. Мы лишь вкратце успеем изложить историю того, как было сделано одно открытие, чтобы показать вам, какого типа рассуждения для этого потребовались. Началось это с открытия Гелл-Манном и Нишиджимой понятия странности и нового закона сохранения странности.

И вот когда Гелл-Манн и Пайс проанализировали следствия из этих новых представлений, то они пришли к предсказанию замечательнейшего явления, о котором мы и хотим повести речь.

Сперва, однако, нужно немного рассказать о «странности».

Начать нужно с того, что называется сильными взаимодейст­виями ядерных частиц. Существуют взаимодействия, которые ответственны за мощные ядерные силы, в отличие, например, от относительно более слабых электромагнитных взаимодейст­вий. Взаимодействия «сильны» в том смысле, что если две части­цы сойдутся так близко, чтобы быть способными взаимодейст­вовать, то взаимодействуют они очень мощно и создают другие частицы очень легко. Ядерные частицы обладают еще так назы­ваемым «слабым взаимодействием», в результате которого происходят такие вещи, как бета-распад; но они всегда происходят очень медленно (по ядерным масштабам времени): слабые взаимо­действия на много-много порядков величины слабее, чем силь­ные, и даже слабее, чем электромагнитные.