Ричард Фейнман - 8a. Квантовая механика I

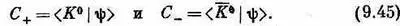
Следующим шагом мы должны написать уравнение Гамиль­тона для такой системы с двумя состояниями. Если бы К 0и 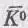не были бы связаны между собой, то уравнения выглядели бы просто

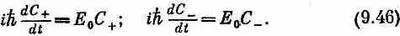
Однако есть еще амплитуда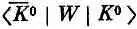

перехода К 0в 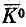; поэтому в правую часть первого уравнения надо еще добавить слагаемое

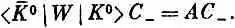
Аналогичное слагаемое АС +надо добавить и в уравнение, опре­деляющее скорость изменения С _. Но это еще не все! Если уж мы учитываем двухпионный эффект, то надо учесть и то, что существует еще дополнительная амплитуда превращения К 0в самого себя по цепочке

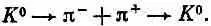
Эта дополнительная амплитуда (обозначим ее 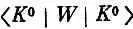)в точности равна амплитуде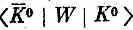

, так как амплитуды перехода в пару p-мезонов или от пары p-мезонов в К 0или 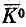одни и те же.

Если угодно, можно показать это и подробнее. Прежде всего напишем

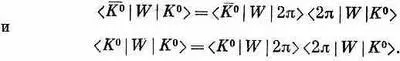
Симметрия между материей и антиматерией требует, чтобы

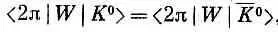
а также

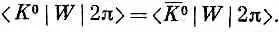
Отсюда

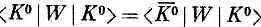
а также

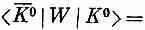
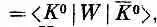
очем мы уже говорили выше.

Итак, у нас есть две дополнительные амплитуды 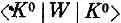и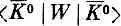

, обе равные А, которые надо вставить в урав­нения Гамильтона. Первая приводит к слагаемому АС + в правой части уравнения для dC + /dt, а вторая — к слагаемому АС - в правой части уравнения для dC - /dt. Рассуждая именно так, Гелл-Манн и Пайс пришли к заключению, что уравне­ния Гамильтона для системы 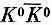должны иметь вид

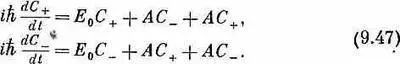
Теперь надо сделать поправку к сказанному в прежних гла­вах: к тому, что две амплитуды, такие, как 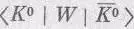и 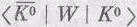, выражающие обратные друг к другу процессы, всегда комплексно сопряжены. Это было бы верно, если бы мы говорили о частицах, которые не распадаются. Но если частицы могут распадаться, а поэтому «пропадать», то амплитуды не обязательно комплексно сопряжены. Значит, равенство (9.44)

не означает, что наши амплитуды суть действительные числа. На самом деле они суть комплексные числа. Поэтому коэффи­циент А комплексный и его нельзя просто включить в энер­гию Е 0 .

Часто, возясь со спинами электронов и тому подобными веща­ми, наши герои знали: такие уравнения означают, что имеется другая пара базисных состояний с особенно простым поведением, которые также пригодны для представления системы . K -частиц. Они рассуждали так: «Возьмем теперь сумму и разность этих двух уравнений. Будем отсчитывать все энергии от Е 0и возьмем для энергии и времени такие единицы, при которых h=1». (Так всегда поступают современные теоретики. Это не меняет, конеч­но, физики, но уравнения выглядят проще.) В результате они получили

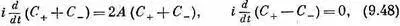
откуда ясно, что комбинации амплитуд С + +С - и С + -С - действуют друг от друга независимо (и отвечают стационарным состояниям, которые мы раньше изучали). Они заключили, что удобнее было бы для K -частиц употреблять другое представле­ние, Они определили два состояния:

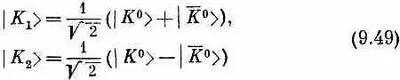
и сказали, что вместо того, чтобы думать о 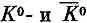-мезонах, с равным успехом можно рассуждать на языке двух «частиц» (т. е. «состояний») К 1и К 2 . (Они, конечно, соответствуют состоя­ниям, которые мы обычно называли | I > и | II >. Мы не поль­зуемся нашими старыми обозначениями, потому что хотим следовать обозначениям самих авторов, тем, которые вы встре­тите на физических семинарах.)

Но Гелл-Манн и Пайс проделывали все это не для того, чтобы давать частицам новые названия; во всем этом имеется еще некоторая весьма странная физика. Пусть C 1и С 2суть амплитуды того, что некоторое состояние |y> окажется либо k 1 -, либо K 2-мезоном:

Из уравнений (9.49)

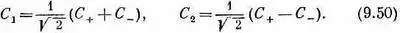
Тогда (9.48) превращается в

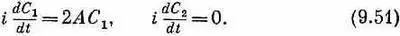
Их решения имеют вид

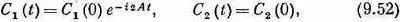
где С 1(0) и С 2(0) — амплитуды при t= 0 .

Эти уравнения говорят, что если нейтральный K -мезон при t= 0 находится в состоянии | К 1> [так что С 1(0)=1 и