Ричард Фейнман - 8a. Квантовая механика I

Полное состояние с определенной энергией |y n( t )> можно тогда записать так:

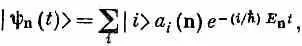
или

Векторы состояний | n> описывают конфигурацию состояний с определенной энергией, но с вынесенной зависимостью от вре­мени. Это постоянные векторы, которые, если мы захотим, можно использовать в качестве новой базисной совокупности.

Каждое из состояний | n> обладает тем свойством (в чем легко убедиться), что при действии на него оператором Гамиль­тона Н получится просто Е n , умноженное на то же состояние:

Значит, энергия Е n — это характеристическое число опера­тора Гамильтона Н^. Как мы видели, у гамильтониана в об­щем случае бывает несколько характеристических энергий. Фи­зики обычно называют их «собственными значениями» мат­рицы Н. Для каждого собственного значения Н^, иными словами, для каждой энергии, существует состояние с определенной энергией, которое мы называли «стационарным». Состояния | n> обычно именуются «собственными состояниями Н^». Каждое собственное состояние отвечает определенному собственному значению Е n .

Далее, состояния | n> (их N штук) могут, вообще говоря, тоже быть выбраны в качестве базиса. Для этого все состояния должны быть ортогональны в том смысле, что для любой нары их, скажем | n> и | m),

< n| m>=0. (9.68)

Это выполнится автоматически, если все энергии различны. Кроме того, можно умножить все а i ( n) на подходящие множи­тели, чтобы все состояния были отнормированы: чтобы для всех nбыло

< n| n>=1. (9.69)

Когда оказывается, что (9.63) случайно имеет два (или боль­ше) одинаковых корня с одной и той же энергией, то появляются небольшие усложнения. По-прежнему имеются две различные совокупности а i , отвечающие двум одинаковым энергиям, но состояния, которые они дают, не обязательно ортогональны. Пусть вы проделали нормальную процедуру и нашли два стацио­нарных состояния с равными энергиями. Обозначим их |m>и |v>. Тогда они не обязательно окажутся ортогональными: если вам не повезло, то обнаружите, что

№0.

Но зато всегда верно, что можно изготовить два новых состоя­ния (обозначим их | m'> и |v'>) с теми же энергиями, но орто­гональных друг другу:

=0. (9.70)

Этого можно добиться, составив |m'> и |v'> из подходящих линейных комбинаций |m> и |v> с так подобранными коэффи­циентами, что (9.70) будет выполнено. Это всегда полезно де­лать, и мы будем вообще предполагать, что это уже проделано, так что можно будет считать наши собственноэнергетические состояния | n> все ортогональными.

Для интереса докажем, что когда два стационарных состоя­ния обладают разными энергиями, то они действительно ортого­нальны. Для состояния | n> с энергией Е n

Это операторное уравнение на самом деле означает, что имеется соотношение между числами. Если заполнить недостающие части, то оно означает то же самое, что и

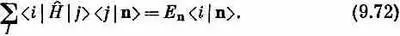
Проделав здесь комплексное сопряжение, получим

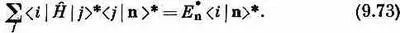
Теперь вспомним, что комплексно сопряженная амплитуда — это амплитуда обратного процесса, так что (9.73) можно пе­реписать в виде

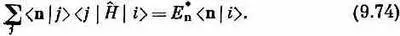
Поскольку это уравнение справедливо для всякого i, то его можно «сократить» до

Это уравнение называется сопряженным с (9.71).

Теперь легко доказать, что Е n — число вещественное. Умножим (9.71) на < n|. Получится

(с учетом, что < n| n>=1). Умножим теперь (9.75) справа на

| n>:

Сравнивая (9.76) с (9.77), видим, что

Е n =Е n *, (9.78)

а это означает, что E nвещественно. Звездочку при Е n в (9.75) можно убрать.

Теперь наконец-то мы в силах доказать, что состояния с различными энергиями ортогональны. Пусть | n> и | m> — пара базисных состояний с определенными энергиями. Написав (9.75) для состояния | m> и умножив его на | n>, получим

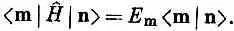
Но если (9.71) умножить на < m|, то будет

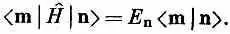
Раз левые части этих уравнений равны, то равны и правые:

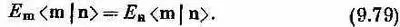
Если Е m =Е n , то это равенство ни о чем не говорит. Но если энергии двух состояний | m> и | n> различны (Е m №Е n ), то урав­нение (9.79) говорит, что < m| n> должно быть нулем, что мы и хотели доказать. Два состояния обязательно ортогональны, если только Е n и Е m отличаются друг от друга.

* Такую интерференцию действительно наблюдали. Коэффициент a оказался равным — 0,96b. Отсюда можно было вычислить и разность масс К 1 - и K 2 -мезонов. Она оказалась равной около —0,35·10 -5 эв. Это наимень­шая разность масс двух частиц, известных физикам.— Прим. ред.

* Мы здесь упрощаем. Система 2p может иметь множество состоя­ний, отвечающих различным импульсам p-мезонов, и в правой части >того равенства следовало бы поставить сумму по всем базисным состоя­ниям p-мезонов. Но полный вывод все равно приводит к тем же резуль­татам.