Ричард Фейнман - 8a. Квантовая механика I

С 2(0)=0], то амплитуды в момент t таковы:

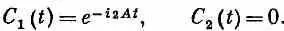
Вспоминая, что А — комплексное число, удобно положить

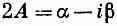
(так как мнимая часть 2А оказывается отрицательной, мы пишем ее как минус ib ). После такой подстановки С 1( t ) принимает вид

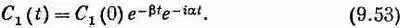
Вероятность обнаружить в момент t частицу К 1равна квадрату модуля этой амплитуды, т. е. e -2 b t . А из (9.52) следует, что ве­роятность обнаружить в любой момент состояние K 2равна нулю. Это значит, что если вы создаете К -мезон в состоянии | К 1>, то вероятность найти его в том же состоянии со временем экспо­ненциально падает, но вы никогда не увидите его в состоянии | К 2> . Куда же он девается? Он распадается на два p-мезона со средним временем жизни t= 1/ 2b, экспериментально равным 10 -1 0 сек. Мы предусмотрели это, говоря, что А комплексное.

С другой стороны, (9.52) утверждают, что если создать . K -мезон целиком в состоянии К 2 , он останется в нем навсегда. На самом-то деле это не так. На опыте замечено, что он распа­дается на три p-мезона, но в 600 раз медленнее, чем при описан­ном нами двухпионном распаде. Значит, имеются какие-то другие малые члены, которыми мы в нашем приближении пренебрегли. Но до тех пор, пока мы рассматриваем только двухпионные распады, К 2остается «навсегда».

Рассказ о Гелл-Манне и Пайсе близится к концу. Дальше они посмотрели, что будет, когда K -мезон образуется вместе с L 0 -частицей в сильном взаимодействии. Раз его странность должна быть +1, он обязан возникать в состоянии К 0 , Значит, при t =0 он не является ни К 1 , ни К 2 , а их смесью. Начальные условия таковы:

Но это означает [из (9.50)], что

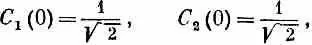
а из (9.52) следует, что

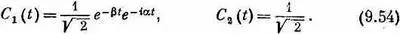
Теперь вспомним, что K 1и К 2суть линейные комбинации К 0и К°. В (9.54) амплитуды были выбраны так, что при t =0 части,

из которых состоит 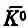, взаимно уничтожаются за счет интер­ференции, оставляя только состояние К 0 . Но состояние | К 1> со временем меняется, а состояние | К 2> — нет . После t= 0 интерференция С 1и С 2приведет к конечным амплитудам и для К 0 , и для .

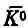Что же все это значит? Возвратимся назад и подумаем об опыте, показанном на фиг. 9.5. Там p --мезон образовал L 0-частицу и K 0-мезон, который летит без оглядки сквозь водород камеры. Когда он движется, существует ничтожный, но постоянный шанс, что он столкнется с ядром водорода. Раньше мы думали, что сохранение странности предохранит K-мезон от образования L 0-частицы в таком взаимодействии. Теперь, однако, мы понимаем, что это не так. Потому что, хотя наш К-мезон вначале является К 0-мезоном, неспособным к рож­дению L°-частицы, он не остается им навечно. Через мгнове­ние появляется некоторая амплитуда того, что он перейдет в состояние 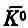. Значит, следует ожидать, что иногда мы увидим L 0-частицу, образованную вдоль следа K -мезона. Вероятность такого происшествия дается амплитудой С - , которую можно [решая (9.50)] связать с С 1и С 2. Связь эта такова:

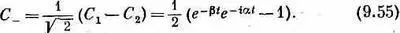
И когда K -частица движется, вероятность того, что она будет «действовать как» 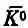, равна | С - | 2 , т. е.

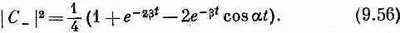
Сложный и поразительный результат!

Это и есть замечательное предсказание Гелл-Манна и Пайса: когда возникает K 0-мезон, то шанс, что он превратится в 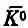- мезон, продемонстрировав это возможностью создания L 0-частицы, меняется со временем по закону (9.56). Это предсказание последовало только из чистейших логических рассуждений и из основных принципов квантовой механики без знания внутрен­них механизмов K -частицы. И поскольку никто не знает ничего об этом внутреннем механизме, то дальше этого Гелл-Манн и Пайс не смогли продвинуться. Им не удалось дать теоретических значений a и b. И никто до сегодняшнего дня не смог это сделать. Им было по силам оценить значение b из экспериментально на­блюдаемой скорости распада на два p-мезона (2b=1,1·10 10 сек -1), но про a они ничего не смогли сказать.

Мы изобразили функцию (9.56) для двух значений a на фиг. 9.6.

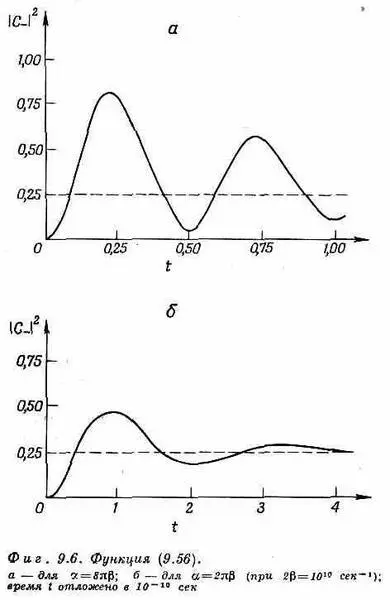
Видно, что форма ее сильно зависит от отношения a и b. Наблюдать 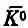-мезон сперва нет никакой вероятности, но затем она появляется. Если значение a велико, вероятность сильно осциллирует; если оно мало, осцилляции невелики или вовсе отсутствуют, вероятность просто плавно возрастает до 1/ 4.

Как правило, K -мезоны движутся с постоянной скоростью, близкой к скорости света. Тогда кривые фиг. 9.6 также пред­ставляют вероятность наблюдения 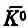-мезона вдоль следа с ти­пичными расстояниями порядка нескольких сантиметров. Те­перь вы видите, отчего это предсказание так удивительно свое­образно. Вы создаете отдельную частицу, и она не просто рас­падается, а проделывает нечто совсем иное. Временами она распадается, а порой превращается в частицу другого сорта. Характеристическая вероятность этого эффекта по мере ее дви­жения меняется очень странно. Ничего другого, похожего на это, в природе нет. И это удивительнейшее предсказание было сделано только на основе рассуждений об интерференции амплитуд.

Если и существует какое-то место, где есть шанс проверить главные принципы квантовой механики самым прямым обра­зом — бывает ли суперпозиция амплитуд или не бывает,— то оно именно здесь. Несмотря на то что этот эффект был предска­зан уже несколько лет тому назад, до сих пор достаточно ясного опытного определения еще не было. Имеются некоторые грубые результаты, указывающие, что значение a не равно нулю и что эффект действительно наблюдается: они свидетельствуют, что a по порядку величины равно b. И это все, что мы знаем из эксперимента. Было бы замечательно, если бы удалось точно проверить и посмотреть, действительно ли работает принцип суперпозиции в этом таинственном мире странных частиц — с неизвестными поводами для распадов и неизвестным поводом существования странности.