Ричард Фейнман - 8a. Квантовая механика I

Всякое состояние может быть представлено линейной комби­нацией |1 > и |2 >(с коэффициентами С 1и С 2) или линейной ком­бинацией базисных состояний с определенной энергией | I > и | II > (с коэффициентами С I и С II ) . Итак,

| Ф >=|1>С 1 +|2>С 2 , или

|Ф>=| I > С I +| II > С II .

Вторая формула дает нам амплитуды обнаружить состоя­ние |Ф> в состоянии с энергией Е I =Е 0 +А или в состоянии с энергией Е II =Е 0 -А.

§ 2. Молекула в статическом электрическом поле

Если молекула аммиака находится в любом из двух состоя­ний определенной энергии, а мы приложим к ней возмущение с частотой w, такой, что hw= E I - Е П =2А, то система может перейти из нижнего состояния в верхнее. Или она может перейти из верхнего в нижнее и испустить фотон. Но для возбуждения таких переходов у вас должна быть физическая связь с состоя­ниями — возможность возмущать систему. Должен существо­вать какой-то внешний механизм влияния на состояния, нечто вроде электрического или магнитного поля. В нашем частном случае эти состояния чувствительны к электрическому полю. На очереди, стало быть, у нас теперь проблема поведения мо­лекулы аммиака во внешнем электрическом поле.

Для разбора этого поведения вернемся опять к перво­начальной базисной системе |1> и |2> вместо | I > и | II >. Пред­положим, что имеется электрическое поле, направленное по­перек плоскости атомов водорода. Пренебрежем на мгновение возможностью переброса атома азота вверх или вниз и зададим вопрос: верно ли, что энергия, этой молекулы в обоих положе­ниях атома азота будет одинаковой? Вообще говоря, нет. Элект­роны стремятся к тому, чтобы находиться ближе к ядру азота, чем к ядрам водорода, так что водороды оказываются слегка положительно заряженными. Насколько — это зависит от деталей расположения электронов. Каково это распределение, точно представить очень трудно, но, во всяком случае, окон­чательный результат состоит в том, что у молекулы аммиака есть электрический дипольный момент, как показано на фиг.7.1. С его помощью можно продолжить дальнейший анализ, не ин­тересуясь деталями направлений или величин смещений за­рядов. Впрочем, чтобы наши обозначения не отличались от общепринятых, предположим, что электрический дипольный момент равен m и направлен от атома азота поперек плоскости атомов водорода.

Далее, когда азот перепрыгивает с одной стороны на дру­гую, то центр масс не перемещается, а электрический дипольный момент переворачивается. В результате энергия в электрическом поле x будет зависеть от ориентации молекулы. При сделанном только что допущении потенциальная энергия бу­дет выше тогда, когда атом азота будет удален от плоскости водородов в направлении поля, и ниже, когда он удален в обратную сторону; промежуток между обеими энергиями будет равен 2mx .

До этого места мы вынуждены были делать предположения о том, чему равны Е 0и А, не зная, как подсчитать их. В соот­ветствии со строгой физической теорией обязана существовать возможность вычисления этих констант, если известны поло­жения и движения всех ядер и электронов. Но никто никогда не делал этого. В систему входит десяток электронов и четверка ядер, и задача чересчур сложна. Факт остается фактом: о молекуле этой никто не знает больше того, что знаем мы с вами. И все, что всякий может о ней сказать,— что в электри­ческом поле энергия двух состояний отличается и разность энергий пропорциональна электрическому полю. Коэффициент пропорциональности мы обозначили 2m, но его величина долж­на определяться экспериментально. Можно еще сказать, что молекула имеет амплитуду А перевернуться, но и она должна измеряться экспериментально. Никто не укажет нам точных теоретических значений m и А , потому что расчеты уж слишком сложны, чтобы честно их проделать.

Для молекулы аммиака в электрическом поле наше описа­ние придется изменить. Если игнорировать амплитуду пере­броса молекулы из одной конфигурации в другую, то энергии двух состояний |1> и | 2 >обязаны быть равны (Е 0±mx) . Сле­дуя процедуре, принятой в предыдущей главе, мы примем

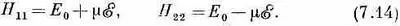
Кроме того, предположим, что при интересующих нас электри­ческих полях сами поля не сказываются заметно на геометрии молекулы и, стало быть, на амплитуде того, что атом азота перепрыгнет из одного положения в другое.

Поэтому можно принять, что Н 12и H 21не изменились, т. е.

H 12= H 21=- А. (7.15)

Теперь с этими новыми значениями Н ij надо решать гамильтоновы уравнения (6.43). Мы могли бы их решить просто, как делали это прежде, но поскольку нам не раз, видимо, представится случай решать системы с двумя состояниями, то давайте уж решим их раз и навсегда в общем случае произвольного Н ij , считая только, что со временем оно не меняется.

Мы ищем общее решение пары гамильтоновых уравнений

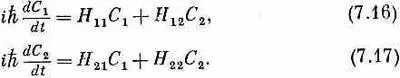
Это линейные дифференциальные уравнения с постоянными коэффициентами. Значит, всегда можно найти решения, яв­ляющиеся экспоненциальными функциями независимой пере­менной t. Сперва отыщем решения, в которых С 1и С 2одина­ково зависят от времени; возьмем пробные функции

Поскольку это решение отвечает состоянию с энергией E=hw ,

то можно прямо написать

где Е пока неизвестна и должна быть определена так, чтобы дифференциальные уравнения (7.16) и (7.17) выполнялись. При подстановке С 1 и С 2из (7.18) и (7.19) в дифференци­альные уравнения (7.16) и (7.17) производные дают просто - iE/h, умноженное на С 1или C 2, так что слева остается попросту ЕС 1или ЕС 2 . Сокращая общие экспоненциальные множители, получаем

или после перестановки членов