Ричард Фейнман - 7. Физика сплошных сред

Они связаны точно таким же образом, как Еи Р, т. е. мы должны писать:

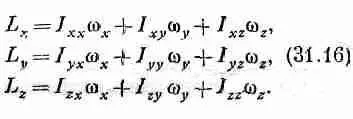
Девять коэффициентов I ij называют тензором инерции. По ана­логии с поляризацией кинетическая энергия для любого мо­мента количества движения должна быть некоторой квадратич­ной формой компонент w x, w yи w z:

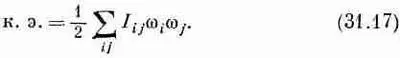
Мы можем снова воспользоваться этим выражением для опре­деления эллипсоида инерции. Кроме того, снова можно восполь­зоваться энергетическими соображениями и показать, что этот тензор симметричен, т. е. I ij =I ji .

Тензор инерции твердого тела можно написать, если извест­на форма тела. Нам нужно только выписать полную кинетиче­скую энергию всех частиц тела. Частица с массой m и скоростью v обладает кинетической энергией 1 / 2 mv 2 , а полная кинетиче­ская энергия равна просто сумме

S 1/ 2mv 2

по всем частицам тела. Но скорость v каждой частицы связана с угловой скоростью wтвердого тела. Предположим, что тело вращается относительно центра масс, который мы будем счи­тать покоящимся. Если при этом r — положение частицы отно­сительно центра масс, то ее скорость v задается выражением wXr. Поэтому полная кинетическая энергия равна

к. э.=S 1/ 2m(wX г) 2. (31.18)

Единственное, что нужно теперь сделать,— это переписать wXr через компоненты w х , w y , w zи координаты х, у, z, а за­тем сравнить результат с уравнением (31.17); приравнивая коэффициенты, найдем I ij . Проделывая всю эту алгебру, мы пишем:

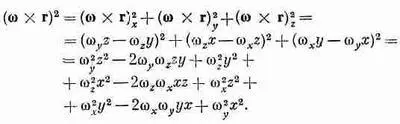
Умножая это уравнение на m/2, суммируя по всем частицам и сравнивая с уравнением (31.17), мы видим, что I xx , напри­мер, равно

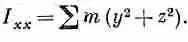
Это и есть та формула для момента инерции тела относительно оси х, которую мы получали уже раньше (гл. 19, вып. 2).

Ну а поскольку r 2 =x 2 +y 2 + z 2, то эту же формулу можно написать в виде

I xx =Sm(r 2 -x 2 ). Выписав остальные члены тензора инерции, получим

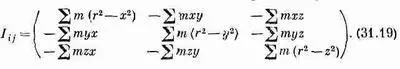
Если хотите, его можно записать в «тензорных обозначе­ниях»:

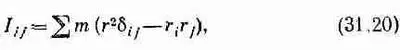
где через r iобозначены компоненты (х, у, z) вектора положе­ния частицы, а 2 означает суммирование по всем частицам. Таким образом, момент инерции есть тензор второго ранга, элементы которого определяются свойствами тела и который связывает момент количества движения Lс угловой ско­ростью w:

Для любого тела независимо от его формы можно найти эл­липсоид энергии, а следовательно, и три главные оси. Относи­тельно этих осей тензор будет диагональным, так что для лю­бого объекта всегда есть три ортогональные оси, для которых момент количества движения и угловая скорость параллельны друг другу. Они называются главными осями инерции.

§ 5. Векторное произведение

Сами того не подозревая, вы пользуетесь тензором второго ранга уже начиная с гл. 20 (вып. 2). В самом деле, мы опреде­лили там «момент силы, действующий в плоскости», например t xy, следующим образом:

t xy =xF y -yF x .

Обобщая это определение на три измерения, можно написать

t ij=r iF j-r jF i. (31.22)

Как видите, величина t ij— это тензор второго ранга. Один из способов убедиться в этом — свернуть t ijс каким-то век­тором, скажем с единичным вектором е, т. е. составить

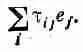
Если эта величина окажется вектором, то t ij должен преобра­зовываться как тензор — это просто наше определение тензора. Подставляя выражение для t ij, получаем

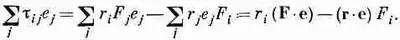
Поскольку скалярные произведения, естественно, являются скалярами, то оба слагаемых в правой части — векторы, как и их разность. Так что t ij-— действительно тензор.

Однако t ijпринадлежит к особому сорту тензоров, он антисимметричен, т. е.

t ij=-t ji.

Поэтому у такого тензора есть только три разные и неравные нулю компоненты: t xy, t yzи t zz. В гл. 20 (вып. 2) нам удалось показать, что эти три члена почти «по счастливой случайности» преобразуются подобно трем компонентам вектора; поэтому мы могли тогда определить вектор

t=(t x,. t y, t z) = (t yz, t zx, t xy).

Я сказал «по случайности» потому, что это происходит только в трехмерном пространстве. Например, для четырех измерений антисимметричный тензор второго ранга имеет шесть различных ненулевых членов, и его, разумеется, нельзя заменить векто­ром, у которого компонент только четыре.

Точно так же как аксиальный вектор t== rX Fявляется тен­зором, по тем же соображениям тензором будет и любое век­торное произведение двух полярных векторов. К счастью, они тоже представимы в виде вектора (точнее, псевдовектора), что немного облегчает нам всю математику.

Вообще говоря, для любых двух векторов аи bдевять ве­личин a i b j образуют тензор (хотя для физических целей он не всегда может быть полезен). Таким образом, для вектора по­ложения r величины r ir jявляются тензором, а поскольку d ij. тоже тензор, то мы видим, что правая часть (31.20) действитель­но является тензором. Подобным же образом тензором будет и (31.22), так как оба члена в правой части — тензоры.

§ 6. Тензор напряжений

Встречавшиеся до сих пор симметричные тензоры возникали как коэффициенты, связывающие один вектор с другим. Сей­час я познакомлю вас с тензором, имеющим совершенно другой физический смысл,— это тензор напряжений. Предположим, что на твердое тело действуют различные внешние силы. Мы говорим, что внутри тела возникают различные «напряжения», имея при этом в виду внутренние силы между смежными частями материала. Мы уже гово­рили немного о подобных на­пряжениях в двумерном случае, когда рассматривали поверхностное натяжение напряженной диафрагмы (см. гл. 12, § 3, вып. 5). А теперь вы увидите, что внутренние силы в материале трехмерного тела записываются в виде тензора.