Ричард Фейнман - 7. Физика сплошных сред

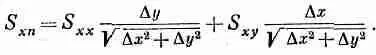
Но, как видно из фиг. 31.8, отношение D х/Ц( D x 2+Dy 2) — это косинус угла q между n и осью у и может быть записан как п у , т. е. y-компонента вектора n. Аналогично, Dy/Ц(Dx 2+Dy 2) равно sinq= n х . Поэтому мы можем написать

S xn =S xx n x +S xy n y

рели теперь обобщить это на произвольный элемент поверхности, то мы получим

S xn= S xxn x+S xyn y+S xzn z,

или в еще более общей форме:

Так что мы действительно можем выразить силу, действующую на произвольную площадь, через элементы S ij и полностью описать внутреннее напряжение.

Уравнение (31.24) говорит, что тензор S ijсвязывает силу S nс единичным вектором nточно так же, как a ijсвязывает Рс Е. Но поскольку nи S n— векторы, то компоненты S ij при изменении осей координат должны преобразовываться как тензор. Так что S ij действительно тензор.

Можно также доказать, что S ij симметричный тензор. Для этого нужно обратить внимание на силы действующие на маленький кубик материале. Возьмем кубик, грани которого параллельны осям координат, и посмотрим на его разрез (фиг. 31.9).

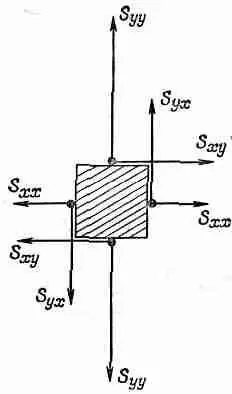
Фиг. 31.9. х- и у-компоненты сил, действующих на четыре грани маленького единичного кубика.

Если допустить что ребра куба равны единице, то х- и y-компоненты сил на гранях, перпендикулярных к осям х и у, должны быть такими, как показано на рисунке. Если взять достаточно маленький кубик, можно надеяться, что напряжение на его противоположных гранях будет отличаться ненамного, а поэтому компоненты сил должны быть равны и противоположны, как это показано на рисунке. Заметьте теперь, что на кубик не должен действовать никакой момент си иначе кубик начал бы вращаться. Но полный момент относительно центра равен произведению (S yx -S xy ) на единичную длину ребра куба, а поскольку полный момент равен нулю, то S должно быть равно S xy, и тензор напряжений, таким образом, оказывается симметричным.

Благодаря этой симметрии тензора S ij его можно то; описывать эллипсоидом с тремя главными осями. Напряжение имеет особенно простой вид на площадках, нормальных к этим: осям: оно соответствует чистому сжатию или растяжению в направлении главных осей. Вдоль этих площадок нет никак сдвиговых сил, причем такие оси, для которых отсутствуют сдвиговые силы, можно выбрать для любого напряжения. Если эллипсоид превращается в сферу, то в любом направлении действуют только нормальные силы. Это соответствует гидростатическому давлению (положительному или отрицательном. Таким образом, для гидростатического давления тензор диагонален, причем все три компоненты его равны друг другу (фактически они просто равны давлению р). В этом случае мы можем написать

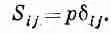(31.25)

Вообще говоря, тензор напряжений в куске твердого тела, а также его эллипсоид изменяются от точки к точке, поэтому для описания всего куска мы должны задать каждую компонен­ту S ij как функцию положения. Тензор напряжений, таким об­разом, является полем. Мы уже имели примеры скалярных по­лей, подобных температуре Т(х, у, z), и векторных полей, по­добных Е (х, у, z), которые в каждой точке задавались тремя числами. А теперь перед нами пример тензорного поля, задавае­мого в каждой точке пространства девятью числами, из кото­рых для симметричного тензора S ij реально остается только шесть. Полное описание внутренних сил в произвольном твер­дом теле требует знания шести функций координат х, у и z.

§ 7. Тензоры высших рангов

Тензор напряжений S ij описывает внутренние силы в веществе. Если при этом материал упругий, то внутренние деформа­ции удобно описывать с помощью другого тензора T ij— так называемого тензора деформаций. Для простого объекта, подоб­ного бруску из металла, изменение длины DL, как вы знаете, приблизительно пропорционально силе, т. е. он подчиняется закону Гука

DL=gF.

Для произвольных деформаций упругого твердого тела тензор деформаций T ij связан с тензором напряжений S ij системой линейных уравнений

Вы знаете также, что потенциальная энергия пружины (или бруска) равна

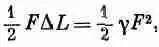
а обобщением плотности упругой энергии для твердого тела будет выражение

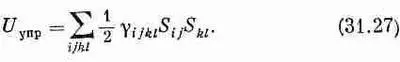
Полное описание упругих свойств кристалла должно задаваться коэффициентами g ijkl. Это знакомит нас с новым зверем — тен­зором четвертого ранга. Поскольку каждый из индексов может принимать одно из трех значений — х, у или z, то всего ока­зывается 3 4=81 коэффициент. Но различны из них на самом де­ле только 21. Во-первых, поскольку тензор S ijсимметричен, у него остается только шесть различных величин, и поэтому в уравнении (31.27) нужны только 36 различных коэффициен­тов. Затем, не изменяя энергии, мы можем переставить S ij и S kl , так что g ijklдолжно быть симметрично при перестановке пары индексов ij и kl. Это уменьшает число коэффициентов до 21. Итак, чтобы описать упругие свойства кристалла низшей воз­можной симметрии, требуется 21 упругая постоянная! Разу­меется, для кристаллов с более высокой симметрией число необходимых постоянных уменьшается. Так, кубический кри­сталл описывается всего тремя упругими постоянными, а для изотропного вещества хватит и двух.

В справедливости последнего утверждения можно убе­диться следующим образом. В случае изотропного материала компоненты g ijkl не должны зависеть от поворота осей. Как это может быть? Ответ: они могут быть независимы, только когда выражаются через тензоры d ij. Но существует лишь два воз­можных выражения, имеющих требуемую симметрию,— это d ijd klи d ikd jl+d il+d jk, так что g ijklдолжно быть их линейной комбинацией. Таким образом, для изотропного материала