Ричард Фейнман - 7. Физика сплошных сред

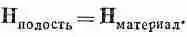
Но поскольку в нашей полости Мравна нулю, то мы полу­чаем

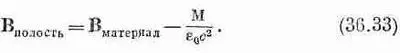
С другой стороны, для дискообразной полости, перпендику­лярной М,

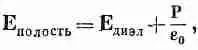
что в нашем случае превращается в

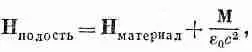
или в величинах В:

Наконец, для сферической полости аналогия с уравнением (36.3) дала бы

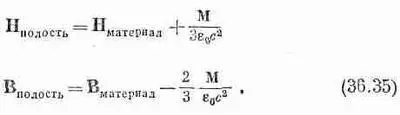
Результаты для магнитного поля, как видите, отличаются от тех, которые мы имели для электрического поля.

Конечно, их можно получить и более физически, непосред­ственно используя уравнения Максвелла. Например, уравне­ние (36.34) непосредственно следует из уравнения С·B=0. (Возьмите гауссову поверхность, которая наполовину находит­ся в материале, а наполовину — вне его.) Подобным же обра­зом вы можете получить уравнение (36.33), воспользовавшись контурным интегралом по пути, который туда идет по полости, а назад возвращается через материал. Физически поле в полос­ти уменьшается благодаря поверхностным токам, определяемым как V X М. На вашу долю остается показать, что уравнение (36.35) можно получить, рассматривая эффекты поверхностных токов на границе сферической полости.

При нахождении равновесной намагниченности из уравне­ния (36.29) удобнее, оказывается, иметь дело с Н, поэтому мы пишем

В приближении сферической полости коэффициент Я следует взять равным 1 / 3 , но, как вы увидите позже, нам придется пользоваться несколько другим его значением, а пока оставим его как подгоночный параметр. Кроме того, все поля мы возь­мем в одном и том же направлении, чтобы нам не нужно было заботиться о направлении векторов. Если бы теперь мы под­ставили уравнение (36.36) в (36.29), то получили бы уравнение, которое связывает намагниченность М с намагничивающим полем Н:

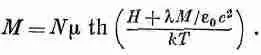
Однако это уравнение невозможно решить точно, так что мы будем делать это графически.

Сформулируем задачу в более общей форме, записывая уравнение (36.29) в виде

где М нас— намагниченность насыщения, т. е. N m , a x — вели­чина m B a /kT. Зависимость М/М нас от х показана на фиг. 36.13 (кривая а).

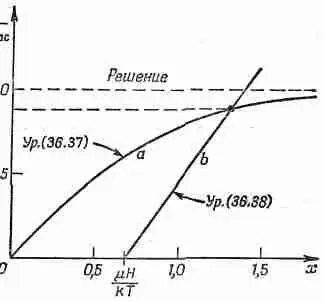
Фиг. 36.13. Графическое реше­ние уравнений (36.37) и (36.38),

Воспользовавшись еще уравнением (36.36) для В а , можно записать х как функцию от М:

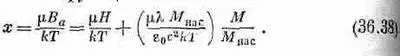
Эта формула определяет линейную зависимость между М/М нас и х при любой величине Н. Прямая пересекается с осью х в точке x=mH/kT, и наклон ее равен e 0 с 2 kT/mlKM нас . Для любого частного зна­чения Н это будет пря­мая, подобная прямой b на фиг. 36.13. Пересечение кривых а и о дает нам решение для М/М нас. Итак, задача решена.

Посмотрим теперь, годны ли эти решения при различных обстоятельствах. Начнем с H =0. Здесь представляются две возможности, показанные кривыми b 1 и b 2 на фиг. 36.14.

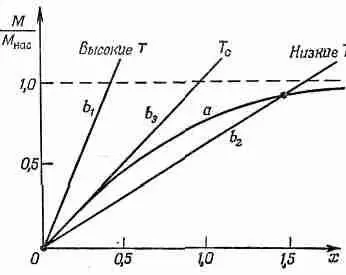
Фиг. 36.14. Определение намагниченности при Н=0.

Обра­тите внимание, что наклон прямой (36.38) пропорционален аб­солютной температуре Т. Таким образом, при высоких темпера­турах получится прямая, подобная b 1 Решением будет только М/М нас=0. Иначе говоря, когда намагничивающее поле Я равно нулю, намагниченность тоже равна нулю. При низких температурах мы получили бы линию типа b 2и стали возможны два решения для М/М нас: одно М/М нас=0, а другое М/М наспорядка единицы. Оказывается, что только второе решение устойчиво, в чем можно убедиться, рассматривая малые вариа­ции в окрестности указанных решений.

В соответствии с этим при достаточно низких температурах магнитные материалы должны намагничиваться спонтанно. Короче говоря, когда тепловое движение достаточно мало, то взаимодействие между атомными магнитиками заставляет их выстраиваться параллельно друг другу, получается постоянно намагниченный материал, аналогичный пос­тоянно поляризованным сегнетоэлектрикам, о которых мы говорили в гл. 11 (вып. 5).

Если мы отправимся от высоких температур и начнем дви­гаться вниз, то при некой критической температуре, называемой температурой Кюри Т c , неожиданно проявляется ферромагнит­ное поведение. Эта температура соответствует на фиг. 36.14 линии b 3 , касательной к кривой а, наклон которой равен еди­нице. Так что температура Кюри определяется из равенства

При желании уравнение (36.38) можно записать в более прос­том виде через Т c :

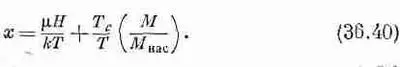
Что же получается для малых намагничивающих полей Н? Из фиг. 36.14 нетрудно понять, что получится, если нашу пря­мую линию сдвинуть немного направо. В случае низкой темпе­ратуры точка пересечения немного сдвинется направо по слабо наклоненной части кривой а и изменения М будут сравнительно невелики. Однако в случае высокой температуры точка пересе­чения побежит по крутой части кривой а и изменения М станут относительно быстрыми. Эту часть кривой мы фактически мо­жем приближенно заменить прямой линией а с единичным наклоном и написать