Ричард Фейнман - 7. Физика сплошных сред

Полагают, что направленный вверх спин одного из электро­нов внутренней оболочки, который ответствен за магнетизм, стремится заставить спины электронов проводимости, витаю­щих вокруг него, повернуться в противоположную сторону. Можно надеяться, что это ему вполне удастся, ибо электроны проводимости движутся в той же самой области, что и «магнит­ные» электроны. А поскольку они движутся то туда, то сюда, то могут передать свой приказ перевернуться «вверх ногами» спинам электронов других атомов; таким образом, «магнитный» электрон заставляет электрон проводимости направить спин в противоположную сторону, а тот в свою очередь заставляет следующий «магнитный» электрон направить свой спин проти­воположно его спину. Это двойное взаимодействие эквивалентно взаимодействию, стремящемуся выстроить два «магнитных» электрона в одном направлении. Иными словами, тенденция соседних спинов быть параллельными есть результат действия промежуточной среды, которая в некотором смысле стремится быть противоположной им обоим. Этот механизм не требует, чтобы все электроны проводимости были повернуты «вверх ногами». Достаточно, чтобы они лишь слегка стремились по­вернуться вниз, и шансы «магнитных» электронов повернуться вверх перевесят. Как полагают те исследователи, которые рабо­тали с этими вещами, это и есть тот механизм, который ответ­ствен за ферромагнетизм. Но должен отметить, что вплоть до сегодняшнего дня никто не может вычислить величину l мате­риала, зная просто, что в периодической системе элементов этот материал стоит, скажем, под номером 26. Короче говоря, мы все еще не можем понять явление до конца.

Теперь же продолжим рассуждения о нашей теории, а потом вернемся снова назад и обсудим некоторые ошибки избранного нами пути. Если магнитный момент какого-то электрона на­правлен вверх, то его энергия частично обусловлена внешним полем, а частично связана с тенденцией спинов быть параллель­ными. Поскольку при параллельных спинах энергия меньше, то эффект получается таким же, как и от «внешнего эффектив­ного поля». Но помните, что обязано это не истинным магнит­ным силам, а более сложному взаимодействию. Во всяком слу­чае, в качестве выражений для энергии двух спиновых состояний «магнитного» электрона мы примем уравнения (37.1). От­носительная вероятность этих двух состояний при температуре Т пропорциональна exp[-энергия/kT], что можно записать как е ±х , где х= | m |(H+lM/e 0с 2)/kT. Если затем мы вычислим среднюю величину магнитного момента, то найдем (как и в предыдущей главе), что она равна

M=N | m |th x. (37.2)

Теперь я могу подсчитать внутреннюю энергию материала. Отметим, что энергия электрона в точности пропорциональна магнитному моменту, так что все равно, вычислять ли средний момент или среднюю энергию. Среднее значение энергии будет при этом

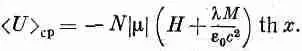
Но это не совсем верно. Выражение lM/e 0c 2представляет взаимодействие всех возможных пар атомов, а мы должны пом­нить, что каждую пару следует учитывать только один раз. (Ког­да мы учитываем энергию одного электрона в поле остальных, а затем энергию второго электрона в поле остальных, то мы еще раз учитываем часть первой энергии.) Поэтому выражение взаи­модействия мы должны разделить на 2 и наша формула для энергии приобретет вид

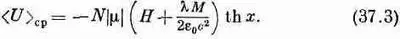
В предыдущей главе мы обнаружили одну очень интересную особенность: для каждого материала ниже определенной темпе­ратуры существует такое решение уравнений, при котором маг­нитный момент не равен нулю даже в отсутствие внешнего на­магничивающего поля. Если в уравнении (37.2) мы положим Н=0, то найдем

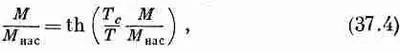
где М нас=N|m| и T c = |m|lM нас ./ke 0 c 2 . Решив это уравнение (графи­чески или каким-то другим способом), мы найдем, что отноше­ние М/М нас как функция от T/T c представляет кривую, наз­ванную на фиг. 37.1 «квантовая теория».

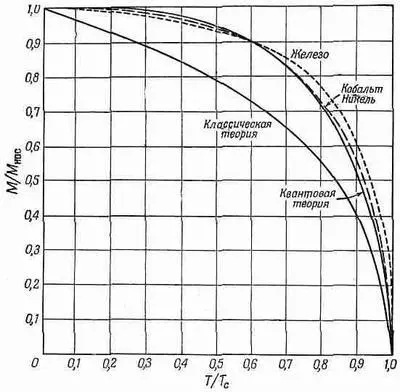
Фиг. 37.1. Зависимость спонтанной намагниченности (Н=0) ферромагнитных кристаллов от температуры.

Пунктирная кривая «Кобальт, Никель» — это полученная экспериментально кри­вая для кристаллов этих элементов. Теория и эксперимент находятся в разумном согласии. Там же представлены резуль­таты классической теории, в которой вычисления проводились в предположении, что атомные магнитики могут иметь всевоз­можные ориентации в пространстве.

Можете убедиться, что это предположение приводит к предсказаниям, которые весьма далеки от экспериментальных данных.

Даже квантовая теория недостаточно хорошо описывает наблюдаемое поведение при высоких и низких температурах. Причина этого отклонения заключена в принятом нами доволь­но грубом приближении: мы предполагали, что энергия атома зависит лишь от средней намагниченности соседних с ним ато­мов. Другими словами, каждый атом со спином, направленным вверх, находящийся по соседству с данным атомом, из-за квантовомеханического эффекта выстраивания вносит свой вклад в энергию. А сколько таких атомов? В среднем это из­меряется величиной намагниченности, но это только в сред­нем. Может оказаться, что для какого-то одного атома спины всех его соседей направлены вверх. Тогда его энергия будет выше средней. У другого же спины некоторых соседей направ­лены вверх, а некоторых — вниз, а среднее может быть нулем, и тогда никакого вклада в энергию вообще не будет и т. д. Из-за того что атомы в разных местах имеют различное окружение с различным числом направленных вверх и вниз спинов, нам следовало бы воспользоваться более сложным способом усред­нения. Вместо того чтобы брать один атом, подверженный сред­нему влиянию, нам следовало бы взять каждый атом в его реаль­ной обстановке, подсчитать его энергию, а затем найти среднюю энергию. Но как же все-таки определить, сколько соседей ато­мов направлено вверх, а сколько — вниз? Это как раз и нужно вычислить, но здесь мы сталкиваемся с очень сложной задачей внутренних корреляций,— задачей, которую никому еще не уда­валось решить. Эта животрепещущая и интригующая проблема в течение многих лет волновала умы физиков; по этому вопросу писалось множество статей крупнейшими учеными, но и они не могли найти полного решения.