Ричард Фейнман - 7. Физика сплошных сред

Оказывается, что при низких температурах, когда почти все атомные магниты направлены вверх и лишь некоторые направ­лены вниз, задача решается довольно легко; то же самое можно сказать и о высоких температурах, значительно превышаю­щих температуру Кюри Т с , когда почти все они направлены совершенно случайно. Часто легко вычислить небольшие откло­нения от некоторой простой идеализированной теории, и до­вольно ясно, почему такие отклонения имеются при низких температурах. Физически понятно, что по статистическим при­чинам намагниченность при высоких температурах должна исчезать. Но точное поведение вблизи точки Кюри никогда во всех подробностях не было установлено. Это очень интересная задача, над которой стоит потрудиться, если когда-нибудь вам вздумается взяться за еще не решенную проблему.

§ 2. Термодинамические свойства

В предыдущей главе мы заложили основу, необходимую для вычисления термодинамических свойств ферромагнитных ма­териалов. Они, естественно, связаны с внутренней энергией кристалла, которая обусловлена взаимодействием между раз­личными спинами и определяется формулой (37.3). Для нахож­дения энергии, связанной со спонтанной намагниченностью (ни­же точки Кюри), мы можем в уравнении (37.3) положить Н=0 и, заметив, что thx=М/М нас, найти, что средняя энергия про­порциональна М 2 :

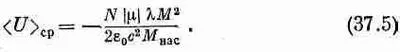
Если мы теперь построим график зависимости намагниченности от температуры, то получим кривую, которая описывается от­рицательным квадратом функции (37.1) и представлена на фиг. 37.2, а. Если бы мы измеряли удельную теплоемкость такого материала, то получили бы кривую (фиг. 37.2, б), ко­торая представляет производную кривой, изображенной на фиг. 37.2, а.

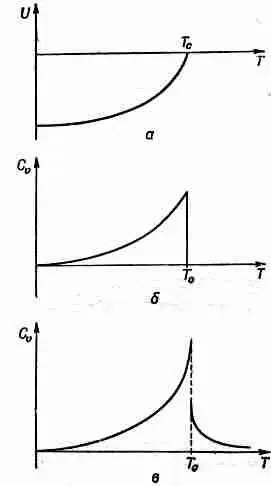
Фиг. 37.2. Энергия в единице объема и удельная теплоемкость ферромагнитного материала.

С увеличением тем­пературы эта кривая медленно растет, но затем при Т = Т с нео­жиданно падает до нуля. Резкое падение вызвано изменением на­клона кривой магнитной энер­гии, и кривая ее производной попадает прямо в точку Кюри. Таким образом, совершенно без магнитных измерений, лишь наб­людая за термодинамическими свойствами, мы бы смогли уста­новить, что внутри железа или никеля что-то происходит. Однако как из эксперимента, так и из улучшенной теории (с учетом внутренних флуктуации) следует, что эти простые кривые неправильны и что истинная картина на самом деле бо­лее сложна. Пик этих кривых поднят выше, а падение до нуля происходит несколько медленнее. Даже если температура до­статочно велика, так что спины в среднем распределены совер­шенно случайно, все равно попадаются области с определенным значением намагниченности, и спины в этих областях продол­жают давать небольшую дополнительную энергию взаимодей­ствия, которая медленно уменьшается с ростом температуры и увеличением беспорядка. Так что реальная кривая выглядит так, как показано на фиг. 37.2, в. Одна из целей физики сегод­няшнего дня — найти точное теоретическое описание удельной теплоемкости вблизи точки перехода Кюри — захватывающая проблема, не решенная до сих пор. Естественно, что эта пробле­ма очень тесно связана с формой кривой намагничивания в той же самой области.

Опишем теперь некоторые эксперименты, отнюдь не термоди­намического характера, которые показывают, что мы все же в каком-то смысле правы в нашей интерпретации магнетизма. Когда материал при достаточно низких температурах намагни­чен до насыщения, то М очень близка к М нас, т. е. почти все спины, равно как и магнитные моменты, параллельны. Это можно проверить экспериментально. Предположим, что мы подвесили магнитную па­лочку на тонкой струне, а затем окружили ее катушкой, так что мо­жем менять магнитное поле, не притрагиваясь к магниту и не прикладывая к нему никакого момента сил. Это очень трудный эксперимент, ибо магнитные силы столь велики, что любая нерегулярность, любой перекос или несо­вершенство в железе могут дать случайный момент. Однако такой эксперимент был выполнен со всей необходимой аккурат­ностью и роль случайных моментов была сведена до минимума. С помощью магнитного поля катушки, которая окружает па­лочку, мы сразу можем перевернуть все магнитные моменты. Когда мы это проделаем, то заодно «сверху вниз» перевернутся и все моменты количества движения, связанные со спином (фиг. 37.3).

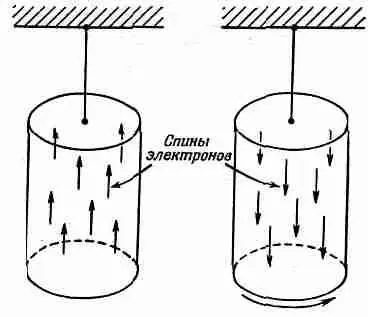
Фиг. 37.3. При перемагничивании железного бруска он приобретает некоторую угловую скорость.

Но поскольку момент количества движения должен сохраняться, то, когда все спины перевернулись, момент количе­ства движения палочки должен измениться в противоположную сторону. Весь магнит должен начать вращаться. Это произошло на самом деле. Когда опыт был проделан, то было обнаружено слабое вращение магнита. Мы можем измерить полный момент количества движения, переданный всему магниту, который про­сто равен произведению N на h и на изменение момента количе­ства движения каждого спина. Оказалось, что измеренное этим способом отношение момента количества движения к магнит­ному с 10%-ной точностью совпадает с нашими вычислениями. На самом деле в наших вычислениях мы исходили из того, что атомный магнетизм целиком обязан электронным спинам, од­нако в большинстве материалов есть еще и орбитальное движе­ние. Орбитальное движение связано с решеткой, но она дает в магнетизм вклад не более нескольких процентов. Действительно, если взять M нас =Nm и для плотности железа взять значение 7,9, а для m—момент электрона, связанный с его спином, то для магнитного поля получим насыщение около 20 000 гс. Однако опыт показывает, что на самом деле оно имеет значение вблизи 21500 гс. Ошибка в 5 или 10% возникает как раз из-за того, что мы пренебрегли вкладами орбитальных моментов. Таким образом, небольшое расхождение с гиромагнитными измерения­ми совершенно понятно.

§ 3. Петля гистерезиса

Из нашего теоретического анализа мы заключили, что маг­нитные материалы ниже некоторой температуры должны ста­новиться спонтанно намагниченными, так что все магнитики в них должны смотреть в одном и том же направлении. Однако для обычного куска ненамагниченного железа это, как мы знаем, неверно. Почему железо не намагничивается все целиком? С помощью фиг. 37.4 я могу объяснить вам это. Допустим, что все железо было бы одним большим кристаллом такой формы, как показано на фиг. 37.4, а, и этот кристалл целиком намаг­нитился бы в одном направлении.