Ричард Фейнман - 7. Физика сплошных сред

Поскольку стенки трубки образуются ли­ниями тока, то жидкость через них не протекает. Обо­значим площадь на одном конце трубки через A 1, скорость жидкости через v 1 , плотность через r 1а потенциальную энер­гию через j 1. Соответствующие величины на другом конце трубки мы обозначим через A 2 , v 2 , r 2и j 2. После короткого интервала времени Dt жидкость на одном конце передвинется на расстояние v 1 D t, а жидкость на другом конце — на расстоя­ние v 2Dt (см. фиг. 40.6, б). Сохранение массы требует, чтобы масса, которая вошла через A 1 была равна массе, которая

вышла через А 2 . Изменение масс в этих двух концах должно быть одинаково:

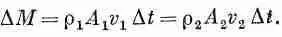
Таким образом, мы получаем равенство

Оно говорит нам, что при постоянном r скорость изменяется обратно пропорционально площади трубки тока.

Вычислим теперь работу, произведенную давлением в жидкости. Работа, произведенная над жидкостью, входящей со стороны сечения А 1 , равна р 1A 1v 1АDt, а работа, произведен­ная в сечении А 2 , равна p 2 A 2 v 2 D t. Следовательно, полная работа, произведенная над жидкостью, заключенной между A 1и А 2 , будет

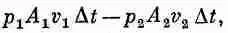
что должно быть равно возрастанию энергии массы жидкости DM при прохождении от А 1 до А 2 . Другими словами,

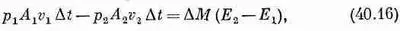
где Е 1 — энергия единицы массы жидкости в сечении А 1 , а Е 2 — энергия единицы массы в сечении А 2 . Энергию единицы массы жидкости можно записать в виде

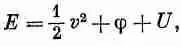
где 1/ 2 v 2 — кинетическая энергия единицы массы, j — потен­циальная энергия, a U — дополнительный член, представляю­щий внутреннюю энергию единицы массы жидкости. Внутрен­няя энергия может соответствовать, например, тепловой энер­гии сжимаемой жидкости или химической энергии. Все эти величины могут изменяться от точки к точке. Воспользо­вавшись выражением для энергии в уравнении (40.16), получим

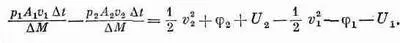
Но мы видели, что DМ=rDvDt, и получили

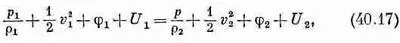
а это как раз приводит нас к результату Бернулли, где имеется дополнительный член, представляющий внутреннюю энергию. Если жидкость несжимаемая, то внутренняя энергия с обеих сторон одна и та же и мы снова убеждаемся в справедливости уравнения (40.14) вдоль любой линии тока.

Рассмотрим теперь неко­торые простые примеры, в которых интеграл Бернулли позволяет нам сразу описать поток. Предположим, что из отверстия вблизи дна резервуара вы­текает вода (фиг. 40.7).

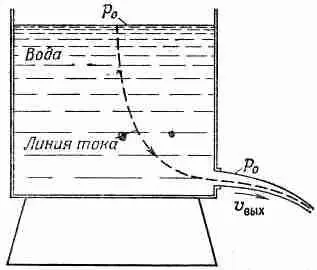
Фиг. 40.7. Вытекание жидкости из резервуара.

Рассмотрим случай, когда скорость пото­ка v выхв отверстии гораздо больше скорости потока вблизи по­верхности воды в резервуаре; другими словами, предположим, что диаметр резервуара настолько велик, что падением уровня жидкости можно пренебречь. (Мы могли бы при желании про­делать и более аккуратные вычисления.) Давление на по­верхность воды в резервуаре равно р 0 (атмосферному давлению), т. е. такое же, как и давление на бока струи. Напишем теперь уравнение Бернулли для линии тока наподобие той, что пока­зана на фиг. 40.7. В верхней части резервуара скорость v мы примем равной нулю; гравитационный потенциал j здесь вы­берем тоже равным нулю. В отверстии же скорость равна v выха j =-gh , так что

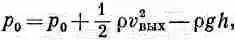
или

Скорость получилась в точности равной скорости предмета, падающего с высоты h. В этом нет ничего удивительного —ведь в конечном счете вода на выходе получает свою кинетическую энергию из запаса потенциальной энергии воды, находящейся наверху резервуара. Однако не воображайте, что вы можете определить скорость убывания жидкости из резервуара, умно­жив эту скорость v выхна площадь отверстия. Скорости частиц жидкости в тот момент, когда струя вырывается из отверстия, не параллельны друг другу, а имеют компоненту, направлен­ную к центру потока; струя сужается. Пройдя небольшое рас­стояние, струя перестает сжиматься, и скорости становятся параллельными. Таким образом, полный поток равен скорости, умноженной на площадь именно в том месте, где сжатие струи прекратилось. На самом деле, если у нас есть выходное отверстие просто в виде круглой дыры с острым краем, то се­чение струи сокращается до 62% от площади отверстия. Уменьшение эффективной площади выходного отверстия для различных форм выходных труб разное, а его экспериментальное значение можно найти в таб­лице коэффициентов истечения.

Если выходная труба вдается в резервуар, как показано на фиг. 40.8, то можно весьма красиво доказать, что коэффи­циент истечения в точности равен 50%. Я лишь намекну вам, как проводится это доказательство.

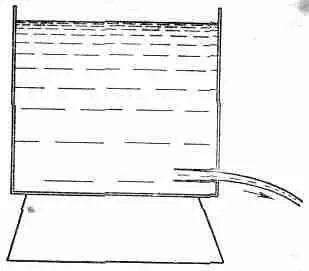
Фиг. 40.8. Если выходная труба вставлена внутрь жидкости, то сокращение струи составляет по­ловину площади отверстия.

Чтобы получить скорость, мы использовали закон сохране­ния энергии [см. уравнение (40.18)]. Можно еще рассмотреть закон сохранения импульса. Поскольку с выходящей струей должен утекать и импульс, то к поперечному сечению выходя­щей трубы должна быть приложена сила. Откуда же она берется? Сила эта должна происходить от давления на стенки. Но наше выходное отверстие мало и расположено далеко от стенок, поэтому скорость жидкости вблизи стенок резервуара будет очень мала. Следовательно, давление на каждую стенку, согласно (40.14), почти точно такое же, как статическое дав­ление в покоящейся жидкости. При этом статическое давление на любую точку с одной стороны резервуара должно урав­новешиваться равным давлением на противоположную стенку, за исключением точки на стороне, противоположной выходной трубе. Если теперь мы вычислим импульс, выталкиваемый со струей этим давлением, то сможем показать, что коэффициент истечения равен 1/ 2. Однако этот метод непригоден для отвер­стия, наподобие показанного на фиг. 40.7, ибо увеличение ско­рости около стенок вблизи области отверстия дает падение давления, которое невозможно вычислить.