Ричард Фейнман - 7. Физика сплошных сред

а наше уравнение движения (40.6) примет вид

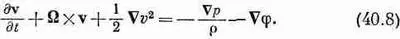
Вы можете проверить эквивалентность уравнений (40.6) и (40.8), расписывая их по компонентам и сравнивая их, восполь­зовавшись при этом выражением (40.7).

Если Wвсюду равно нулю, то такой поток мы называем безвихревым (или потенциальным). В гл. 3, § 5 (вып. 5), мы уже определяли величину, называемую циркуляцией векторного поля. Циркуляция по любой замкнутой петле в жидкости равна криволинейному интегралу от скорости жидкости в дан­ный момент времени вокруг этой петли:

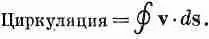
Циркуляция на единицу площади для бесконечно малой петли по теореме Стокса будет тогда равна СX v. Таким образом, Wпредставляет собой циркуляцию вокруг единичной площади (перпендикулярной направлению W). Кроме того, ясно, что если в любое место жидкости поместить маленькую соринку (именно соринку, а не бесконечно малую точку), то она будет вращаться с угловой скоростью W/2. Попытайтесь доказать это. Вы можете также попробовать доказать, что для ведра воды на вращающемся столике Wравна удвоенной локальной угловой скорости воды.

Если нас интересует только поле скоростей, то из наших уравнений можно исключить давление. Взяв ротор обеих частей уравнения (40.8) и вспомнив, что r — величина постоян­ная, а ротор любого градиента равен нулю, а также использо­вав уравнение (40.3), находим

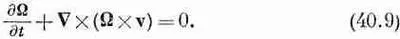
Это уравнение вместе с уравнениями

W=СXv (40.10)

и

С·v=0 (40.11)

полностью описывают поле скоростей v. На языке матема­тики — если в некоторый момент мы знаем W,то мы знаем ротор вектора скорости и, кроме того, знаем, что его дивер­генция равна нулю, так что в этих физических условиях у нас есть все необходимое для определения скорости v по­всюду. (Все это в точности напоминает нам знакомые условия в магнетизме, где С· B=0 и СX B= j/e 0c 2.) Таким образом, данная величина W определяет v точно так же, как jопреде­ляет В. Затем из известного значения v уравнение (40.9) даст нам скорость изменения W, откуда мы можем получить новую W в следующий момент. Используя снова уравнение (40.10), найдем новое значение v и т. д. Теперь вы видите, как в эти уравнения входит весь механизм, необходимый для вычисления потока. Заметьте, однако, что эта процедура дает только ско­рости, а всю информацию о давлении мы потеряли.

Отметим особое следствие нашего уравнения. Если в ка­кой-то момент времени t повсеместно W=0, то дW/дt тоже исче­зает, так что W всюду останется равной нулю и в момент t +Dt. Отсюда следует, что поток все время остается безвихре­вым. Если вначале поток не вращался, то он так никогда и не начнет вращаться. При этом уравнения, которые мы должны решать, таковы:

С·v=0, СXv=0.

Они в точности напоминают уравнения электростатики или магнитостатики в пустом пространстве. Позднее мы вернемся к ним и рассмотрим некоторые частные задачи.

§ 3. Стационарный поток; теорема Бернулли

Вернемся к уравнениям движения (40.8), но ограничимся теперь приближением «стационарного» потока. Под стационарным потоком я подразумеваю поток, скорость которого в любом месте жидкости никогда не изменяется. Жидкость в любой точке постоянно заменяется новой жидкостью, движущейся в точности таким же образом. Кар­тина скоростей всегда выглядит одинаково, т. е. v представ­ляет статическое векторное поле. Как в магнитостатике мы рисовали силовые линии, так и здесь можно начертить линии, которые всегда касательны к скорости жидкости (фиг. 40.5).

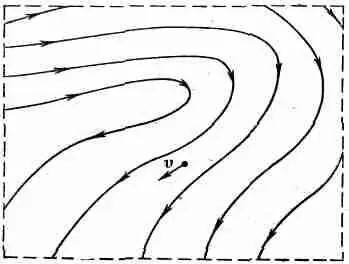
Фиг. 40.5. Линии тока ста­ционарного потока.

Эти линии называются «линиями тока». Для стационарного потока они действительно представляют реальные пути частиц жидкости. (В нестационарном потоке картина линий тока меняется со временем, однако в любой момент времени она не представляет пути частиц жидкости.)

Стационарность потока вовсе не означает, что ничего не происходит — частички жидкости движутся и изменяют свои скорости. Это означает только то, что дv/дt=0. Если теперь мы скалярно умножим уравнение движения на v, то слагаемое v·(WXv) выпадет и у нас останется только

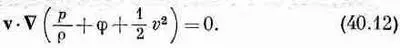
Согласно этому уравнению, при малых перемещениях в направ­лении скорости жидкости величина внутри скобок не изме­няется. В стационарном потоке все перемещения направлены вдоль линий тока; поэтому уравнение (40.12) говорит, что для всех точек вдоль линии тока

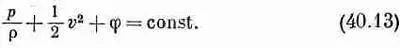
Это и есть теорема Бернулли. Постоянная, вообще говоря, для различных линий тока может быть разной; мы знаем только, что левая часть уравнения (40.13) постоянна всюду вдоль данной линии тока. Заметьте, кстати, что если стационарный поток безвихревой, т. е. если для него W=0, то уравнение движения (40.8) дает нам соотношение

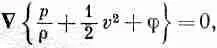
так что

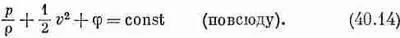
Оно в точности напоминает уравнение (40.13), за исключением того, что теперь постоянная во всей жидкости одна и та же. На самом деле теорема Бернулли не означает ничего боль­шего, чем утверждение о сохранении энергии. Подоб­ные теоремы о сохранении дают нам массу информации о потоке без детального решения уравнений. Теорема Бернулли на­столько важна и настолько проста, что мне бы хотелось пока­зать вам, как можно ее получить другим способом, отличным от тех формальных вычислений, которые мы только что про­вели. Представьте себе пучок линий тока, образующих трубку тока (фиг. 40.6, а).

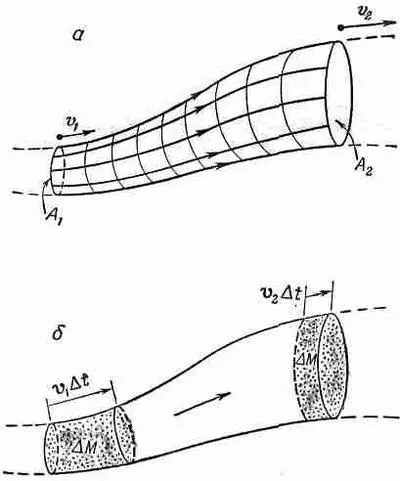
Фиг. 40.6. Движение жидкости в трубке.