Ричард Фейнман - 6a. Электродинамика

Наша программа состоит в том, чтобы повторить в четырех­мерном пространстве-времени все то, что мы делали с векто­рами в трех измерениях. Дело это нехитрое — мы просто будем действовать аналогично. Единственное затруднение встретится только при обозначениях (символ вектора у нас уже занят трех­мерными векторами), и несколько изменятся знаки в скалярном произведении.

Прежде всего, по аналогии с векторами в трехмерном про­странстве, введем четырехвектор как набор четырех величин a t , а х , а у и а z, которые при переходе в движущуюся систему коор­динат преобразуются подобно t, x, у и z. Для обозначения четырехвектора используется несколько различных способов. Мы же будем писать просто а m, понимая под этим группу четырех ве­личин (a t , a x , a y , a z ); другими словами, значок m принимает ка­кое-либо из четырех «значений»: t, x, у и г. Иногда нам будет удобно обозначать три пространственные компоненты в виде трехмерного вектора, т. е. писать a m =(a t , а).

Мы уже сталкивались с одним таким четырехвектором, со­стоящим из энергии и импульса частицы (см. гл. 17, вып. 2). В наших новых обозначениях он запишется так:

p m =(Е, p ), (25.2)

т. е. четырехвектор p mсостоит из энергии Е и трех компонент трехмерного импульса частицы р.

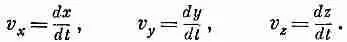
Похоже, что игра действительно оказывается нехитрой: единственное, что мы должны сделать,— это найти для каждого трехмерного вектора недостающую компоненту и получить четырехвектор. Однако все же эта задача потруднее, чем кажется на первый взгляд. Возьмем, например, вектор скорости с компонентами

Что будет его временной компонентой? Инстинкт подсказывает нам, что поскольку четырехвектор подобен t, x , у, z, то времен­ной компонентой как будто должно быть

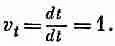
Но это неверно. Дело в том, что время t в каждом знаменателе не инвариантно при преобразованиях Лоренца. Числитель имеет правильное поведение, a dt в знаменателе портит все дело: оно не одинаково в двух различных системах.

Оказывается, что четыре компоненты «скорости», которые нам нужно выписать, превратятся в компоненты четырехвектора, если мы попросту поделим их на Ц(1-v 2 ). В правильности этого можно убедиться, взяв

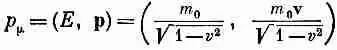
четырехвектор импульса

(25.3)

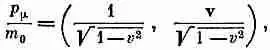
и поделив его на массу покоя, которая в четырехмерном прост­ранстве является скаляром. Мы получим при этом

(25.4)

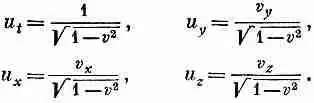
что по-прежнему должно быть четырехвектором. (Деление на скаляр не изменяет трансформационных свойств.) Так что четырехвектор скорости v m можно определить так:

(25.5)

Это очень полезная величина; мы можем теперь написать, например,

(25.6)

Таков типичный вид, который должен иметь правильное реляти­вистское уравнение: каждая сторона его должна быть четырехвектором. (В правой части стоит произведение инварианта на четырехвектор, которое по-прежнему есть четырехвектор.)

§ 2. Скалярное произведение

То, что расстояние от некоторой точки до начала координат не изменяется при повороте, если хотите,— счастливая случай­ность. Математически это означает, что r 2=x 2+y 2+z 2является инвариантом. Другими словами, после поворота r' 2=r 2или

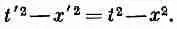
Возникает вопрос: существует ли подобная величина, которая инвариантна при преобразованиях Лоренца? Да, существует. Из (25.1) вы видите, что

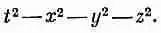
Она была бы всем хороша, если бы только не зависела от наше­го выбора оси х. Но этот недостаток легко исправить вычита­нием y/ 2и z 2. Тогда преобразование Лоренца плюс вращение оставляют ее неизменной. Таким образом, роль величины, ана­логичной трехмерному r 2в четырехмерном пространстве, играет комбинация

Она является инвариантом так называемой «полной группы Лоренца», которая включает как перемещения с постоянной скоростью, так и повороты.

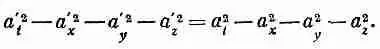
Далее, поскольку эта инвариантность представляет собой алгебраическое свойство, зависящее только от правил преобра­зования (25.1) плюс вращение, то она справедлива для любого четырехвектора. (Все они, по определению, преобразуются оди­наковым образом.) Так что для любого четырехвектора а m

Эту величину мы будем называть квадратом «длины» четырехвектора а м . (Будьте внимательны! Иногда берут обратные зна­ки у всех слагаемых и квадратом длины называют число a 2 x +a 2 y +a 2 z -a 2 t )

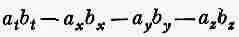
Если теперь у нас есть два вектора а mи b m , то их одноименные компоненты преобразуются одинаково, поэтому комбинация

также будет инвариантной (скалярной) величиной. (Фактически мы доказали это уже в гл. 17, вып. 2.) Получилась величина, совершенно аналогичная скалярному произведению векторов. Мы так и будем называть ее скалярным произведением двух четырехвекторов. Логично, казалось бы, и записывать его а m ·b m , чтобы оно даже выглядело похожим на скалярное произведение. Но обычно, к сожалению, так не делают и пишут его без точки.

И мы тоже будем придерживаться этого порядка и записывать скалярное произведение просто a m b m . Итак, по определению,

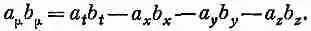
(25.7)

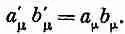
Помните, что повсюду, где вы видите два одинаковых значка (вместо m мы иногда будем пользоваться v или другими бук­вами), необходимо взять четыре произведения и сложить их, не забывая при этом о знаке минус перед произведениями про­странственных компонент. С учетом такого соглашения инва­риантность скалярного произведения при преобразованиях Ло­ренца можно записать как