Ричард Фейнман - 6. Электродинамика
- Название:6. Электродинамика
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 6. Электродинамика краткое содержание
6. Электродинамика - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Наконец, в формуле (21.1) имеется еще третье слагаемое — вторая производная единичного вектора е r '. Изучая явление света, мы по существу использовали тот факт, что вдали от заряда два первых слагаемых убывают как обратный квадрат расстояния и на больших расстояниях оказываются слишком слабыми по сравнению с третьим, которое убывает как 1/r. Поэтому мы сосредоточили наше внимание на последнем слагаемом и показали, что оно (опять-таки на больших расстояниях) пропорционально компоненте ускорения заряда, поперечной к линии зрения. (Кроме того, почти всюду ранее мы рассматривали только случай, когда заряды двигались нерелятивистски. Релятивистские эффекты рассматривались только в гл. 34, вып. 3.)
Теперь нужно попробовать связать эти две вещи. У нас есть уравнения Максвелла и есть формула (21.1) для поля точечного заряда. Естественно спросить, эквивалентны ли они? Если мы сможем вывести (21.1) из уравнений Максвелла, то действительно поймем связь света с электромагнетизмом. Вывод ее и есть главная цель этой главы.
Выясняется, что полного вывода мы сделать не можем — чересчур сложные математические детали не позволят нам выйти с поля боя без потерь. Но все же мы подойдем к цели достаточно близко, так что вы легко поймете, как может быть установлена интересующая нас связь. Мы опустим лишь некоторые математические детали. Математика этой главы может показаться некоторым из вас довольно сложной, и, возможно, вам даже станет скучно следить внимательно за выводом. Но мы все же считаем, что очень важно связать то, что вы учили раньше, с тем, что вы изучаете сейчас, или по крайней мере продемонстрировать, как эта связь может быть установлена. Если вы не забыли прежние главы, то обратите внимание на то, что всякий раз, как мы принимали некоторое высказывание за исходную точку обсуждения, мы заботливо объясняли, является ли это высказывание новым «допущением», т. е. отражает ли оно основной закон природы или же его можно в конечном счете вывести из каких-то других законов. Дух этих лекций обязывает нас обсудить связь менаду светом и уравнениями Максвелла. Может быть, вам будет кое-где и трудно — с этим уж ничего не поделаешь: другого пути не существует.
§ 2. Сферические волны от точечного источника
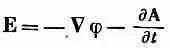
В гл. 18 мы установили, что уравнения Максвелла можно решать подстановкой
(21.2)
и
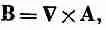
(21.3)
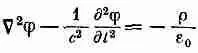
где j и А обязаны удовлетворять уравнениям
(21.4)
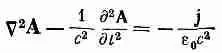
и
(21.5)
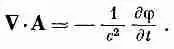
и, кроме того, условию
(21.6)
Найдем теперь решение уравнений (21.4) и (21.5). Для этого надо уметь решать уравнение
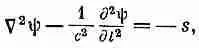
(21.7)
где величина s (которая называется источником) известна. Ясно, что для уравнения (21.4) s соответствует r/e 0, a ш—это j, а для уравнения (21.5) s соответствует j x/e 0с 2, если ш — это А х , и т. д. Но нас интересует чисто математическая задача решения (21.7) безотносительно к тому, каков физический смысл ш и s. Там, где r и j равны нулю (это место называется «пустотой»), там потенциалы j и А и поля Е и В удовлетворяют трехмерному волновому уравнению без источников; математическая форма этого уравнения такова:
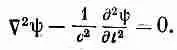
(21.8)
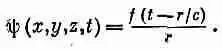
В гл. 20 мы видели, что решения этого уравнения могут представлять волны разных сортов: плоские волны, бегущие в x-направлении я|;=f(t-x/с); плоские волны, бегущие вдоль у или вдоль z или в любом другом направлении; сферические
(21.9)
(Решения можно записать иначе — например в виде цилиндрических волн, разбегающихся от оси.)
Мы тогда заметили, что физически формула (21.9) относится не совсем к пустоте: в начале координат должны быть какие-то заряды, иначе расходящаяся волна не получилась бы. Иными словами, формула (21.9) есть решение уравнения (21.8) всюду, кроме непосредственной окрестности точки r=0, где (21.9) представляет собой решение полного уравнения (21.7), в правой части которого стоят источники. Давайте теперь посмотрим, что это за уравнение, т. е. какого рода источник s в уравнении (21.7) должен вызвать волну типа (21.9).

Предположим, что имеется сферическая волна (21.9) и поглядим, во что она превращается при очень малых r. Тогда запаздыванием -r /с в f(t-r /с) можно пренебречь, и поскольку функция f плавная, ш превращается в
(21.10)
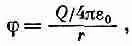
Итак, ш в точности похоже на кулоново поле заряда, расположенного в начале координат. Мы знаем, что для небольшого сгустка заряда, ограниченного очень малой областью близ начала координат и имеющего плотность r,
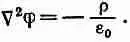
где Q=∫rdV . Такой потенциал j удовлетворяет уравнению
Следуя тем же расчетам, мы должны были бы сказать, что ш из выражения (21.10) удовлетворяет уравнению
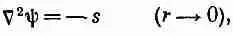
(21.11)
где s связано с f формулой
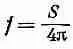
при
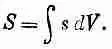
Единственная разница в том, что в общем случае s, а, стало быть, и S может оказаться функцией времени.
Далее очень важно то, что если ш удовлетворяет (21.11) при малых r , то оно удовлетворяет также и (21.7). По мере приближения к началу координат зависимость шот r типа 1/r приводит к тому, что пространственные производные становятся очень большими. А производные по времени остаются теми же. [Это просто производные f(t) по времени.] Так что, когда r стремится к нулю, множителем d 2 ш/dt 2 в уравнении (21.7) по сравнению с С 2ш можно пренебречь, и (21.7) становится эквивалентным уравнению (21.11).
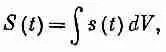
Интервал:
Закладка:




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/1068056/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov.webp)
