Ричард Фейнман - 6. Электродинамика

Подытоживая, можно сказать, что если функция источника s(t) из уравнения (21.7) сосредоточена в начале координат и ее общая величина равна

(21.12)

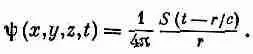
то решение уравнения (21.7) имеет вид

(21.13)

Влияние слагаемого с d 2 ш/dt 2 в (21.7) сказывается лишь на появ­лении запаздывания (t-r/с) в потенциале кулонова типа.

§ 3. Общее peшeниe уравнений Максвелла

Мы нашли решение уравнения (21.7) для «точечного» источ­ника. Теперь встает новый вопрос: Каков вид решения для рас­средоточенного источника? Ну, это решить легко; всякий источ­ник s(x, у, z, t) можно считать состоящим из суммы многих «точечных» источников, расположенных поодиночке в каждом элементе объема dV и имеющих силу s(x, у, z, t)dV. Поскольку (21.7) линейно, суммарное поле представляет собой суперпози­цию полей от всех таких элементов источника.

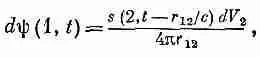
Используя результаты предыдущего параграфа [см. (21.13)], мы получим, что в момент t поле dm в точке (х 1 , y 1,z 1) [или, короче, в точке (1)], создаваемое элементом источника sdV в точке (х 2> у 2 , z 2 ) [или, короче, в точке (2)],выражается форму­лой

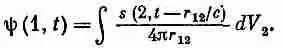
где r 12 — расстояние от (2) до (1). Сложение вкладов от всех частей источника означает, конечно, интегрирование по всей области, где s№0, так что мы имеем

(21.14)

Иначе говоря, поле в точке (1) в момент времени t представляет собой сумму всех сферических волн, испускаемых в момент t-r 12/c всеми элементами источника, расположенного в точке (2). Выражение (21.14) является решением нашего волнового уравнения для любой системы источников.

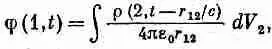
Теперь мы видим, как получать общее решение уравнений Максвелла. Если подразумевать под шскалярный потенциал j, то функция источника s превращается в r/e 0. А можно считать, что ш представляет одну из трех компонент векторного потен­циала А; тогда s означает соответствующую компоненту j/e 0c 2. Стало быть, если во всех точках известна плотность нарядов r (х, у, z, t) и плотность тока j (х, у, z, t), то решения уравнении (21.4) и (21.5) можно выписать немедленно:

(21.15)

(21.16)

Поля Е и В получатся дифференцированием потенциалов [используются выражения (21.2) и (21.3)]. Кстати, можно про­верить явно, что j и А, полученные из (21.15) и (21.16), дей­ствительно удовлетворяют равенству (21.6).

Мы решили уравнения Максвелла. В любых обстоятель­ствах, если только заданы токи и заряды, из этих интегралов можно определить потенциалы, а затем, продифференцировав их, получить поля. Тем самым с теорией Максвелла покончено. И это позволяет нам также замкнуть круг и вернуться к нашей теории света, потому что достаточно только подсчитать элек­трическое поле движущегося заряда, чтобы связать все это с нашей прежней теорией света. Все, что нам остается сделать,— это взять движущийся заряд, вычислить из этих интегралов его потенциал и затем из -Сj- dA/dt, дифференцируя, найти Е. Мы должны получить формулу (21.1). Работы придется проде­лать много, но принцип ясен.

Итак, мы дошли до центра электромагнитной вселенной. У нас в руках полная теория электричества, магнетизма и света, полное описание полей, создаваемых движущимися зарядами, и многое, многое другое. Все сооружение, воздвигнутое Максвел­лом, во всей его полноте, красе и мощи сейчас перед нами. Это, пожалуй, одно из величайших свершений физики. И чтобы напомнить о его важности, мы переписываем все формулы вместе и обводим их красивой рамкой.

§ 4. Поля колеблющегося диполя

Мы пока еще не провели обещанного вывода формулы (21.1) для электрического поля движущегося точечного заряда. Даже зная то, что мы уже знаем, этот вывод все равно проделать не­легко. Нам не удалось обнаружить формулы (21.1) нигде, ни в каких книжках и статьях (кроме первых выпусков этих лек­ций). Это свидетельствует о том, что вывод ее не прост. (Поля движущегося заряда записывались неоднократно и в других видах, которые все, конечно, эквивалентны.) Мы ограничимся поэтому здесь тем, что просто покажем на нескольких приме­рах, что (21.15) и (21.16) приводят к тем же результатам, что и (21.1). Первым делом мы покажем, что при том единственном условии, что движение заряженной частицы является нереля­тивистским, (21.1) приводит к правильной величине полей. (Уже этот частный случай покрывает 90% всего того, что было сказано о явлении света.)

Рассмотрим такую ситуацию, когда имеется сгусток заря­дов, каким-то образом перемещающийся в небольшой обла­сти; требуется найти создаваемые им где-то вдалеке от этого места поля.

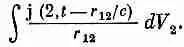
Можно поставить вопрос и иначе: мы найдем поле на произвольном расстоянии от точечного заряда, который почти незаметно колеблется вверх и вниз. Поскольку свет обычно испускают такие нейтральные тела, как атомы, то мы будем считать, что наш колеблющийся заряд q расположен вблизи неподвижного, равного по величине, но противоположного по знаку заряда. Если расстояние между центрами зарядов рав­но d, то у зарядов появится дипольный момент p=qd,который мы будем считать функцией времени. Следует ожидать, что поблизости от зарядов запаздыванием поля можно будет прене­бречь; электрическое поле будет в точности таким же, как и то, которое получалось раньше для электростатического диполя [но, конечно, с мгновенным дипольным моментом p(t)]. Однако при большом удалении в формуле для поля должно появиться добавочное слагаемое, которое меняется как 1/r и зависит от того, каково ускорение заряда в направлении, поперечном к лучу зрения. Посмотрим, получится ли у нас этот результат. Начнем с вычисления векторного потенциала А при помощи (2.16). Пусть плотность зарядов в сгустке есть r(х, у, z) и весь он движется все время со скоростью v. Тогда плотность тока j(x, у, z) равна vr(x,y, z). Удобно систему координат располо­жить так, чтобы ось z была направлена по v; тогда геометрия нашей задачи изобразится так, как показано на фиг. 21.2. Нас интересует интеграл