Ричард Фейнман - 5b. Электричество и магнетизм

(12.19)

где коэффициент диффузии D дается в терминах средней ско­рости v и средней длины свободного пробега l между столкно­вениями:

Векторное уравнение для J имеет вид

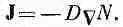
(12.20)

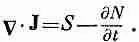
Скорость, с которой нейтроны проходят через некоторый элемент поверхности da, равна J· nda (где n, как обычно,— единичный вектор нормали). Результирующий поток из эле­мента объема тогда равен (пользуясь обычным гауссовым доказательством) С·J dV. Этот поток приводил бы к уменьше­нию числа нейтронов в DV, если нейтроны не генерируются внутри DV (с помощью какой-нибудь ядерной реакции). Если в объеме присутствуют источники, производящие S нейтронов в единицу времени в единице объема, то результирующий поток из DV будет равен [S-(dNIdt)] DV. Тогда получаем

(12.21)

Комбинируя (12.21) и (12.20), получаем уравнение диффузии нейтронов

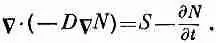
(12.22)

В статическом случае, когда dN/dt=0, мы снова имеем урав­нение (12.4)! Мы можем воспользоваться нашими знаниями в электростатике для решения задач по диффузии нейтронов. Давайте же решим какую-нибудь задачу. (Пожалуй, вы недо­умеваете: зачем решать новую задачу, если мы уже решили все задачи в электростатике? На этот раз мы можем решить быстрее именно потому, что электростатические задачи дей­ствительно уже решены!)

Пусть имеется блок материала, в котором нейтроны (ска­жем, за счет деления урана) рождаются равномерно в сфери­ческой области радиусом а (фиг. 12.7). Мы хотели бы узнать, чему равна плотность нейтронов повсюду? Насколько однород­на плотность нейтронов в области, где они рождаются? Чему равно отношение нейтронной плотности в центре к нейтронной плотности на поверхности области рождения? Ответы найти легко. Плотность нейтронов в источнике S 0 стоит вместо плот­ности зарядов r, поэтому наша задача такая же, как задача об однородно заряженной сфере. Найти N— все равно, что найти потенциал j. Мы уже нашли поля внутри и вне однородно заряженной сферы; для получения потенциала мы можем их проинтегрировать. Вне сферы потенциал равен Q/4pe 0r, где полный заряд Q дается отношением 4pа 3r/3. Следовательно,

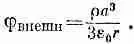
(12.23)

Для внутренних точек вклад в поле дают только заряды Q(r), находящиеся внутри сферы радиусом r ; Q(r) =4pг 3r/3, следовательно,

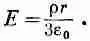
(12.24)

Поле растет линейно с r. Интегрируя Е, получаем j:

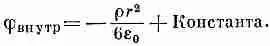
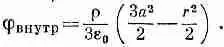
На расстоянии радиуса а j внешндолжен совпадать с j внутр) поэтому постоянная должна быть равна rа 2/2e 0. (Мы предпола­гаем, что потенциал j равен нулю на больших расстояниях от источника, а это для нейтронов будет отвечать обращению .N в нуль.) Следовательно,

(12.25)

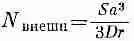
Теперь мы сразу же найдем плотность нейтронов в на­шей диффузионной задаче

(12.26)

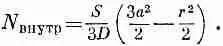
и

(12.27)

На фиг. 12.7 представлена зависимость N от r.

Чему же теперь равно отношение плотности в центре к плотности на краю? В центре (r=0) оно пропорционально За 2/2, а на краю (r=а) пропорционально 2а 2/2; поэтому отно­шение плотностей равно 3/2. Однородный источник не дает однородной плотности нейтронов. Как видите, наши познания в электростатике дают хорошую затравку для изучения физики ядерных реакторов.

Диффузия играет большую роль во многих физических об­стоятельствах. Движение ионов через жидкость или электро­нов через полупроводник подчиняется все тому же уравнению. Мы снова и снова приходим к одним и тем же уравнениям.

§ 5. Безвихревое течение жидкости; обтекание шара

Рассмотрим теперь пример, по существу, не такой уж хоро­ший, потому что уравнения, которые мы будем использовать, на самом деле не описывают новый объект полностью, а отве­чают лишь некоторым идеализированным условиям. Это задача о течении воды. Когда мы разбирали случай натянутой плен­ки, то наши уравнения представляли приближение, справед­ливое лишь для малых отклонений. При рассмотрении течения воды мы прибегнем к приближению другого рода; мы должны принять ограничения, которые, вообще говоря, к обычной воде неприменимы. Мы разберем только случай постоянного тече­ния несжимаемой, невязкой, лишенной завихрений жидкости. Потом мы опишем течение, задав ему скорость v(r) как функцию положения г. Если движение постоянно (единственный случай, для которого имеется электростатическая аналогия), v не за­висит от времени. Если r — плотность жидкости, то rv — масса жидкости, проходящая в единицу времени через единичную площадку. Из закона сохранения вещества дивергенция pv, вообще говоря, равна изменению со временем массы вещества в единице объема. Мы предположим, что процессы непрерыв­ного рождения или уничтожения вещества отсутствуют. Сохра­нение вещества требует тогда, чтобы С·rv=0. (В правой части должно было бы стоять, вообще говоря, — d r /dt, но поскольку наша жидкость несжимаема, то r меняться не может.) Так как r повсюду одинаково, то его можно вынести, и наше уравнение запишется просто

С·v=0.

Чудесно! Снова получилась электростатика (без зарядов); уравнение совсем похоже на С·E=0. Ну не совсем! В электро­статике не просто С·E=0. Есть два уравнения. Одно уравне­ние еще не дает нам всего; нужно дополнительное уравнение. Чтобы получилось совпадение с электростатикой, у нас rot от v должен был бы равняться нулю. Но для настоящих жид­костей это вообще не так. В большинстве их обычно возникают вихри. Следовательно, мы ограничиваемся случаем, когда циркуляция жидкости отсутствует. Такое течение часто назы­вают безвихревым. Как бы то ни было, принимая наши пред­положения, можно представить себе течение жидкости, ана­логичное электростатике. Итак, мы берем

С·v=0 (12.28)

и

СXv = 0. (12.29)

Мы хотим подчеркнуть, что условия, при которых течение жидкости подчиняется этим уравнениям, встречаются весьма нечасто, но все-таки бывают. Это должны быть случаи, когда поверхностным натяжением, сжимаемостью и вязкостью можно пренебречь и когда течение можно считать безвихревым. Эти условия выполняются столь редко для обычной воды, что мате­матик Джон фон Нейман сказал по поводу тех, кто анализи­рует уравнения (12.28) и (12.29), что они изучают «сухую воду»!