Ричард Фейнман - 5b. Электричество и магнетизм

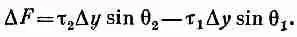
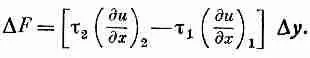
Мы ограничимся рассмотрением малых искажений мембраны, т. е. малых изгибов и наклонов: тогда мы сможем заменить sinq на tgq и записать как дu/дx. Сила при этих условиях дается выражением

Величина в скобках может быть с тем же успехом записана (для малых Dx:) как

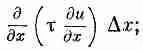
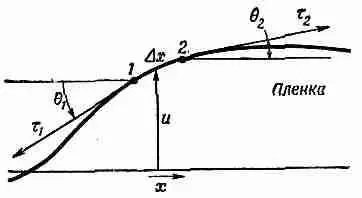
Фиг. 12.5. Поперечное сечение изогнутой пленки.

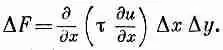
Тогда

Имеется и другой вклад в D F от сил на двух других сторо­нах; полный вклад, очевидно, равен

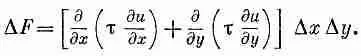
(12.16)

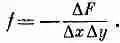
Искривления диафрагмы вызваны внешними силами. Пусть / означает направленную вверх силу на единичную площадку пленки (своего рода «давление»), возникающую от внешних сил. Если мембрана находится в равновесии (статический случай), то сила эта должна уравновешиваться только что вычисленной внутренней силой [уравнение (12.16)]. Иначе говоря,

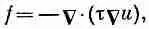
Уравнение (12.16) тогда может быть записано в виде

(12.17)

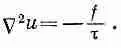
где под знаком Смы теперь подразумеваем, конечно, двух­мерный оператор градиента (д/дх, д/ду). У нас есть дифферен­циальное уравнение, связывающее u(х, у) с приложенными си­лами f(x, у) и поверхностным натяжением пленки t(x, у), которое, вообще говоря, может меняться от места к месту. (Деформации трехмерного упругого тела тоже подчиняются таким уравнениям, но мы ограничимся двухмерным случаем.) Нас будет интересовать только случай, когда натяжение t постоянно по всей пленке. Тогда вместо (12.17) мы можем запи­сать

(12.18)

Снова мы получили такое же уравнение, как в электроста­тике! Но на сей раз оно относится к двум измерениям. Сме­щение u соответствует j, а f/t соответствует r/e 0. Поэтому тот труд, который мы потратили на бесконечные заряженные плос­кости, или параллельные провода большой длины, или заряжен­ные цилиндры, пригодится для натянутой мембраны.

Предположим, мы подтягиваем мембрану в каких-то точках на определенную высоту, т. е. фиксируем величину и в ряде точек. В электрическом случае это аналогично заданию определенного потенциала в соответствующих местах. На­пример, мы можем устроить положительный «потенциал», если подопрем мембрану предметом, который имеет такое же сечение, как и соответствующий цилиндрический проводник. Если, скажем, мы подопрем мембрану круглым стержнем, поверхность примет форму, изображенную на фиг. 12.6.

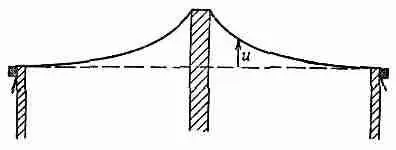
Фиг. 12.6. Поперечное сечение натянутой рези­новой пленки, подпертой круглым стержнем.

Функция u(х, у) та же, что и потенциал j (х, у) от очень длинного заряженного стержня.

Высота и имеет такой же вид, как электростатический потенциал j заряженного цилиндрического стержня. Она спадает, как ln(1/r). (Наклон поверхности, который соответствует электри­ческому полю Е, спадает, как 1/r.)

Натянутую резиновую пленку часто использовали для ре­шения сложных электрических задач экспериментальным путем. Аналогия используется в обратную сторону! Для подъема мембраны на высоту, соответствующую потенциалам всего набора электродов, подставляют разные стержни и полоски. Затем измерения высоты дают электрический потенциал в электростатической задаче. Аналогия проводится даже еще дальше. Если на мембране поместить маленькие шарики, то их движение примерно схоже с движением электронов в соответ­ствующем электрическом поле. Таким способом можно воочию проследить за движением «электронов» по их траекториям. Этот метод был использован для проектирования сложной системы многих фотоумножительных трубок (таких, например, какие используются в сцинтилляционном счетчике или для управления передними фарами в автомашине кадиллак). Метод используется и до сих пор, но его точность не очень велика. Для более точных расчетов лучше находить поле чис­ленным путем с помощью больших электронных вычислитель­ных машин.

§ 4. Диффузия нейтронов; сферически-симметричный источник в однородной среде

Приведем еще один пример, дающий уравнение того же вида, но на сей раз относящееся к диффузии. В гл. 43 (вып. 4) мы рассмотрели диффузию ионов в однородном газе и диффузию одного газа сквозь другой. Теперь возьмем другой пример — диффузию нейтронов в материале типа графита. Мы выбрали графит (разновидность чистого углерода), потому что углерод не поглощает медленных нейтронов. Нейтроны путешествуют в нем свободно. Они проходят по прямой в среднем несколько сантиметров, прежде чем рассеются ядром и отклонятся в сто­рону. Так что если у нас есть большой кусок графита толщи­ной в несколько метров, то нейтроны, находившиеся сначала в одном месте, будут переходить в другие места.

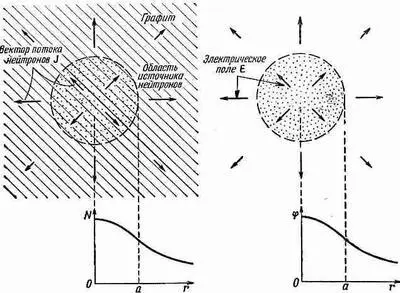
Фиг. 12.7. Нейтроны рождаются однородно внутри сферы радиуса а в большом графитовом блоке и диффундируют наружу. Плотность нейтронов N получена как функция r, расстояния от центра источника.

Справа показана электростатическая аналогия: однородно заряженная сфе­ра, причем N соответствует j, а J соответствует Е.

Мы опишем их усредненное поведение, т. е. их средний поток.

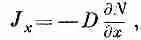
Пусть N(x, у, z)DV — число нейтронов в элементе объема DV в точке (х, у, г). Движение нейтронов приводит к тому, что одни покидают DV, а другие попадают в него. Если в одной области оказывается нейтронов больше, чем в соседней, то от­туда их будет переходить во вторую область больше, чем наобо­рот; в результате возникнет поток. Повторяя доказательства, приведенные в гл. 43 (вып. 4), можно описать поток вектором потока J. Его компонента J x есть результирующее число ней­тронов, проходящих в единицу времени через единичную пло­щадку, перпендикулярную оси х. Мы получим тогда