Ричард Фейнман - 5b. Электричество и магнетизм

Условие, что С·J= 0, означает, что у нас могут быть только заряды, текущие по замкнутым путям. Они могут, например, течь по проводам, образующим замкнутые петли, которые назы­ваются цепями. Цепи могут, конечно, содержать генераторы или батареи, поддерживающие ток зарядов. Но в них не должно быть конденсаторов, которые заряжаются или разря­жаются. (Мы, конечно, расширим теорию, включив перемен­ные поля, но сначала мы хотим взять более простой случай постоянных токов.)

Обратимся теперь к уравнениям (13.12) и (13.13) и посмот­рим, что они означают. Первое говорит, что дивергенция В равна нулю. Сравнивая его с аналогичным уравнением электро­статики, по которому С·Е=r/e 0, можно заключить, что маг­нитного аналога электрического заряда не существует. Не бы­вает магнитных зарядов, из которых могли бы исходить ли­нии В. Если говорить о «линиях» векторного поля В, то они нигде не начинаются и нигде не оканчиваются. Но тогда откуда же они берутся? Магнитные поля «появляются» в присутствии токов; ротор, взятый от них, пропорционален плотности тока. Когда есть токи, есть и линии магнитного поля, образующие петли вокруг токов. Поскольку линии В не имеют ни конца, ни начала, они часто возвращаются в исходную точку, образуя замкнутые петли. Но могут возникнуть и более сложные случаи, когда линии не представляют собой простых петель. Однако как бы они ни шли, они никогда не исходят из точек. Никаких магнитных зарядов никто никогда не находил, поэтому С·В=0. Это же утверждение справедливо не только для маг­нитостатики, но справедливо всегда — даже для динамических полей.

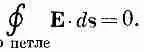
Связь между полем В и токами дается уравнением (13.13). Положение здесь совсем другое, в корне отличное от элек­тростатики, где у нас было СXЕ = 0. Это уравнение означало, что линейный интеграл от Е по любому замкнутому пути равен нулю:

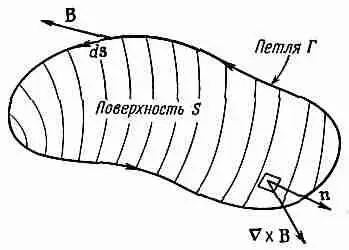
Фиг. 13.6. Контурный интег­рал от тангенциальной со­ставляющей В равен поверхно­стному интегралу от нормаль­ной составляющей вектора

(СX B).

Мы получили этот результат с помощью теоремы Стокса, со­гласно которой интеграл по любому замкнутому пути от любого векторного поля равен поверхностному интегралу от нормаль­ной компоненты ротора этого вектора (интеграл берется по дюбой поверхности, натянутой на данный контур). Применяя эту же теорему к вектору магнитного поля и используя обо­значения, показанные на фиг. 13.6, получаем

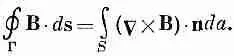
(13.14)

Найдя rot В из уравнения (13.13), имеем

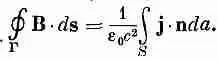
(13.15)

Интеграл от j по S, согласно (13.5), есть полный ток I через поверхность S. Поскольку для постоянных токов ток через S не зависит от формы S, если она ограничена кривой Г, то обыч­но говорят о «токе через замкнутую петлю Г». Мы имеем, та­ким образом, общий закон: циркуляция В по любой замкнутой кривой

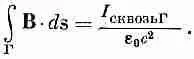
равна току I сквозь петлю, деленному на e 0с 2:

(13.16)

Этот закон, называемый законом Ампера, играет такую же роль в магнитостатике, как закон Гаусса в электростатике. Один лишь закон Ампера не определяет В через токи; мы долж­ны, вообще говоря, использовать также С·В=0. Но, как мы увидим в следующем параграфе, он может быть использован для нахождения поля в тех особых случаях, которые обладают некоторой простой симметрией.

§ 5. Магнитное поле прямого провода и соленоида; атомные токи

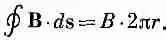
Можно показать, как пользоваться законом Ампера, опреде­лив магнитное поле вблизи провода. Зададим вопрос: чему равно поле вне длинного прямолинейного провода цилиндри­ческого сечения? Мы сделаем одно предположение, может быть, не столь уж очевидное, но тем не менее правильное: линии поля В идут вокруг провода по окружности. Если мы сделаем такое предположение, то закон Ампера [уравнение (13.16)] говорит нам, какова величина поля. В силу симметрии задачи поле В имеет одинаковую величину во всех точках окружности, концентрической с проводом (фиг. 13.7). Тогда можно легко взять линейный интеграл от B·ds. Он равен просто величине В, умноженной на длину окружности. Если радиус окружности равен r , то

Полный ток через петлю есть просто ток I в проводе, поэтому

или

(13.17)

Напряженность магнитного доля спадает обратно пропорцио­нально r, расстоянию от оси провода. При желании уравнение (13.17) можно записать в векторной форме. Вспоминая, что В направлено перпендикулярно как I, так и r, имеем

(13.18)

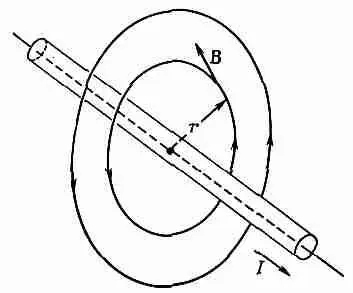
Фиг. 13.7. Магнитное поле вне длинного провода с током I.

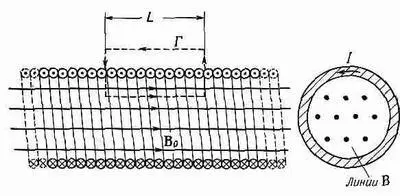
Фиг. 13.8. Магнитное поле длинного соленоида.

Мы выделили множитель 1/4pe 0с 2, потому что он часто по­является. Стоит запомнить, что он равен в точности 10 -7(в си­стеме единиц СИ), потому что уравнение вида (13.17) исполь­зуется для определения единицы тока, ампера. На расстоянии 1 м ток в 1a создает магнитное поле, равное 2·10 -7 вебер/м 2 .

Раз ток создает магнитное поле, то он будет действовать с некоторой силой на соседний провод, по которому также про­ходит ток. В гл. 1 мы описывали простой опыт, показывающий силы между двумя проводами, по которым течет ток. Если про­вода параллельны, то каждый из них перпендикулярен полю В другого провода; тогда провода будут отталкиваться или при­тягиваться друг к другу. Когда токи текут в одну сторону, провода притягиваются, когда токи противоположно направле­ны,— они отталкиваются.

Возьмем другой пример, который тоже можно проанализи­ровать с помощью закона Ампера, если еще добавить кое-какие сведения о характере поля. Пусть имеется длинный провод, свернутый в тугую спираль, сечение которой показано на фиг. 13.8. Такая спираль называется соленоидом. На опыте мы наблюдаем, что когда длина соленоида очень велика по сравнению с диаметром, то поле вне его очень мало по сравне­нию с полем внутри. Используя только этот факт и закон Ам­пера, можно найти величину поля внутри.