Ричард Фейнман - 5b. Электричество и магнетизм

Если выбрать начало отсчета в центре петли, так что А можно считать направленным по касательной и функцией толь­ко от r', то циркуляция будет равна

Как и раньше, получаем

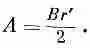
В только что разобранном примере мы вычисляем вектор­ный потенциал из магнитного поля, обычно поступают наоборот. В сложных задачах всегда проще найти векторный потенциал, а затем уже из него найти магнитное поле. Сейчас мы покажем, как это можно сделать.

§ 2. Векторный потенциал заданных токов

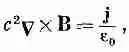
Раз В определяется токами, значит, и А тоже. Мы хотим теперь выразить А через токи. Начнем с нашего основного уравнения (14.2):

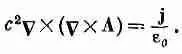
откуда, конечно, следует

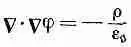
Это уравнение для магнитостатики; оно похоже на уравнение

(14.13)

для электростатики.

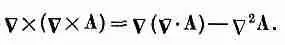
Наше уравнение (14.12) для векторного потенциала ста­нет еще более похожим на уравнение для j, если перепи­сать СX(СX А), используя векторное тождество [см. уравне­ние (2.58) стр. 44]

(14.14)

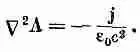
Поскольку мы выбрали С·А=0 (и теперь вы видите, по­чему), уравнение (14.12) приобретает вид

(14.15)

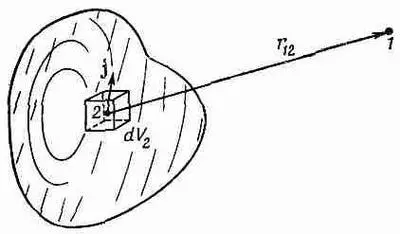
Фиг. 14.2. Векторный потенциал А в точке 1 определяется интегралом по элементам тока jdV во всех точках 2.

Это векторное уравнение, конечно, распадается на три урав­нения

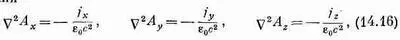
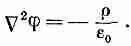
и каждое из этих уравнений математически идентично уравнению

(14.17)

Все, что мы узнали о нахождении потенциала для извест­ного r, можно использовать для нахождения каждой компо­ненты А, когда известно j!

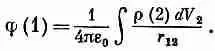
В гл. 4 мы видели, что общее решение уравнения элект­ростатики (14.17) имеет вид

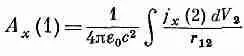
Тогда мы немедленно получаем общее решение для А x :

(14.18)

и аналогично для А у и A z . (Фиг. 14.2 напоминает вам о при­нятых нами обозначениях для r 12и dV 2 .) Мы можем объ­единить все три решения в векторной форме:

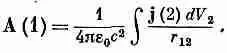
(14.19)

(Вы можете при желании проверить прямым дифференцирова­нием компонент, что этот интеграл удовлетворяет С·А=0, поскольку С·j=0, а последнее, как мы видели, должно вы­полняться для постоянных токов.)

Мы имеем, таким образом, общий метод вычисления маг­нитного поля от постоянных токов. Принцип такой: x-компонента векторного потенциала, возникающая от плотности тока j, точно такая же, как электрический потенциал j, который был бы создан плотностью зарядов р, равной j x /c 2 , и ана­логично для у- и z-компонент. (Этот принцип действует только для декартовых компонент. Например, «радиальная» компо­нента А не связана таким же образом с «радиальной» компонен­той j.) Итак, из вектора плотности тока j можно найти А, пользуясь уравнениями (14.19), т. е. мы находим каждую ком­поненту А, решая три воображаемые электростатические зада­чи для распределений заряда r 1=j x/с 2, r 2=j у/с 2и r 3=j z/с 2. Затем мы находим В, вычислив разные производные от А, входящие в ухА. Немного сложнее, чем в электростатике, но идея та же. Сейчас мы проиллюстрируем теорию, вычислив векторный потенциал в нескольких частных случаях.

§ 3. Прямой провод

В качестве первого примера снова вычислим поле прямого провода, которое мы находили в предыдущем параграфе, поль­зуясь уравнением (14.2) и соображениями симметрии. Возьмем длинный прямой провод радиуса а, по которому течет постоян­ный ток I. В отличие от заряда в проводнике в случае электро­статики постоянный ток в проводе распределен равномерно по поперечному сечению провода. При таком выборе координат, как показано на фиг. 14.3, вектор плотности тока j имеет только z-компоненту. По величине она равна

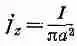
(14.20)

внутри провода и нулю вне его.

Поскольку j х и j yоба равны нулю, то сразу же получим

А х = 0, А у = 0.

Чтобы получить А г , мож­но использовать наше ре­шение для электростати­ческого потенциала j от провода с однородной плотностью заряда r=/ г/с 2.

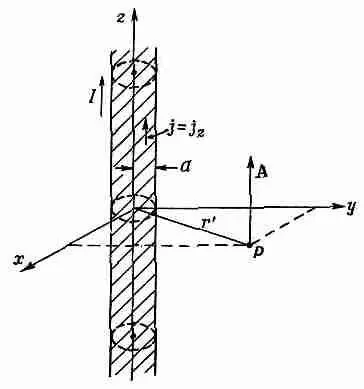
Фиг. 14.3. Длинный цилинд­рический провод с однородной плотностью тока j, направлен­ный вдоль оси z.

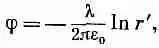
Для точек вне бесконечного заряженного цилиндра электростатический потенциал равен

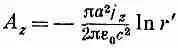
где r'=Ц(x 2+y 2), a l, — заряд на единицу длины pа 2r. Следо­вательно, А г должно быть равно

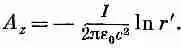
для точек вне длинного провода с равномерно распределен­ным током. Поскольку pа 2j z=I то можно также написать

(14.21)

Теперь можно найти В, пользуясь (14.4). Из шести про­изводных от нуля отличны только две. Получаем

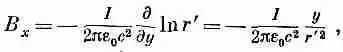
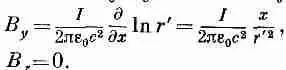
(14.22)

,(14.23)

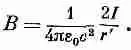
Мы получаем тот же результат, что и раньше: В обходит про­вод по окружности и по величине равен

(14.24).

§ 4. Длинный соленоид

Еще пример. Рассмотрим опять бесконечно длинный соле­ноид с током по окружности, равным пI на единицу длины. (Мы считаем, что имеется n витков проволоки на единицу дли­ны, несущих каждый ток I, и пренебрегаем небольшими зазо­рами между витками.)