Ричард Фейнман - 4a. Кинетика. Теплота. Звук

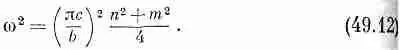
Возьмем теперь для примера прямоугольник, ширина ко­торого вдвое больше высоты. Если положить а=2b и восполь­зоваться уравнениями (49.4) и (49.9), то можно вычислить ча­стоты всех гармоник

В табл. 49.1 перечислено несколько простых гармоник и ка­чественно показана их форма.

Таблица 49.1 · ПРОСТЫЕ ГАРМОНИКИ И ИХ ФОРМА

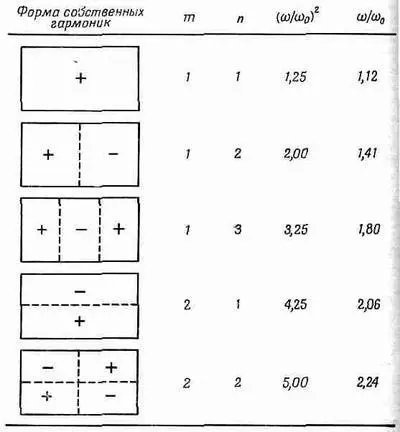
Следует отметить наиболее важную особенность этого част­ного случая — частоты не кратны ни друг другу, ни какому-то другому числу. Представление о том, что собственные частоты гармонически связаны друг с другом, в общем случае неверно. Оно неверно ни для системы размерности, большей единицы, ни даже для одномерной системы, более сложной, чем однород­ная и равномерно натянутая струна. Простейшим примером может служить подвешенная цепочка, натяжение которой вверху меньше, чем внизу. Если возбудить в такой цепочке гармонические колебания, то возникнут собственные гармо­ники с различными частотами, однако частоты не будут просто кратными какому-то числу, да и сама форма гармоник больше не будет синусоидальной.

Еще причудливей оказываются гармоники более сложных систем. Человеческий рот, например, представляет собой по­лость, расположенную над голосовыми связками. Движением языка и губ можно создать либо трубу с открытым концом, либо трубу с закрытым концом, причем диаметры и формы этой трубы будут раз личными. В общем это страшно сложный резона­тор, но тем не менее все же резонатор. При разговоре мы с помощью голосовых связок создаем какой-то тон. Тон этот довольно сложен, в него входит множество звуков, но благо­даря различным резонансным частотам полость рта еще больше модифицирует его. Певец, например, может петь различные гласные: «а», «о», «у» и еще другие с той же самой высотой, но звучат они по-разному, ибо различные гармоники по-разному резонируют в этой полости. Огромную роль резонансных ча­стот полости в образовании голосовых звуков можно проде­монстрировать на очень простом опыте. Как известно, скорость звука обратно пропорциональна квадратному корню из плот­ности, поэтому для разных газов она различна. Если вместо воздуха мы используем гелий, плотность которого меньше, то скорость звука в нем окажется больше и все резонансные ча­стоты полости будут больше. Следовательно, если бы мы могли перед тем, как начать говорить, наполнить наши легкие ге­лием, то, хотя голосовые связки по-прежнему колебались бы с той же частотой, характер нашего голоса резко изменился бы.

§ 4. Связанные маятники

Напоследок необходимо подчеркнуть, что гармоники возни­кают не только в сложных непрерывных системах, но и в очень простых механических системах. Хорошим примером этого служит рассмотренная в предыдущей главе система двух свя­занных маятников. Там мы показали, что общее движение этой системы можно рассматривать как суперпозицию двух типов гармонических движений с различными частотами, так что даже такую систему можно рассматривать с точки зрения собствен­ных гармоник. В струне возбуждается бесконечное число соб­ственных гармоник, у двумерной поверхности их тоже беско­нечно много. В каком-то смысле здесь получается даже двойная бесконечность (если бы мы только знали, как работать с бесконечностями!). Но в простом механическом устройстве, обла­дающем только двумя степенями свободы и требующем для своего описания лишь двух переменных, возбуждаются всего две гар­моники.

Попробуем найти математически эти две гармоники для слу­чая, когда длины маятников одинаковы. Пусть отклонение одного маятника будет х, а другого — y, как это показано на фиг. 49.5.

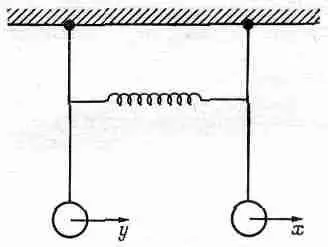
Фиг. 49.5. Два связанных маят­ника.

При отсутствии пружины сила тяжести, действующая на первый маятник, пропорциональна его отклонению. Если бы здесь не было пружины, то для одного маятника появилась бы некоторая собственная частота w 0, а уравнение движения в этом случае приобрело бы вид

m(d 2x/dt 2)=-mw 2 0x . (49.13)

Второй маятник при отсутствии пружины качался бы точно так же, как и первый. Однако при наличии пружины в допол­нение к восстанавливающей силе, возникающей в результате гравитации, появляется еще добавочная сила от пружины, ко­торая стремится «стянуть» маятники. Эта сила зависит от пре­вышения отклонения х над отклонением у и пропорциональна их разности, т. е. она равна некоторой постоянной, зависящей только от геометрии, умноженной на (х-у). Та же сила, но в обратном направлении действует на второй маятник. Поэтому уравнения движения, которые мы должны решить, будут сле­дующими:

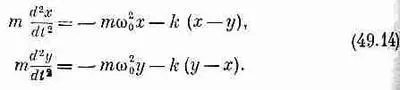
Чтобы найти движение, при котором оба маятника колеблются с одинаковой частотой, мы должны определить, насколько отклоняется каждый из них. Другими словами, маятник А и маятник В будут колебаться с одинаковой частотой и с ка­кими-то амплитудами А и B , отношение которых фиксировано. Давайте проверим, насколько подходит такое решение:

x=Ae i w t , у=Ве i w t . (49.15)

Если подставить его в уравнения (49.14) и собрать подобные члены, то получим

При выводе этих уравнений мы сократили общий множитель е i w t и разделили все на m .

Теперь мы видим, что получились два уравнения для, каза­лось бы, двух неизвестных. Однако на самом деле здесь не два неизвестных, ибо общие масштабы движения нельзя найти из этих уравнений. Они могут дать нам только отношение А к В, причем оба уравнения должны дать одинаковую величину. Тре­бование согласованности уравнений друг с другом накладывает требование на частоту: она должна быть какой-то очень спе­циальной.

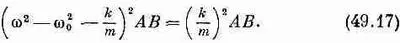
Но найти частоту в этом частном случае довольно легко. Если перемножить оба уравнения, то мы получим

В обеих сторонах можно сократить произведение АВ, за исклю­чением тех случаев, когда либо А, либо В равно нулю, что означает отсутствие движения вообще. Но если движение есть, то должны быть равны между собой и другие сомножи­тели, что приводит к квадратному уравнению. В результате получаются две возможные частоты: