Ричард Фейнман - 4a. Кинетика. Теплота. Звук
- Название:4a. Кинетика. Теплота. Звук
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - 4a. Кинетика. Теплота. Звук краткое содержание
4a. Кинетика. Теплота. Звук - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Можно отметить еще одну, третью сторону этого интересного открытия: оно касается двух нот, которые звучат приятно для слуха. Но далеко ли ушли мы от Пифагора в понимании того, почему только некоторые звуки приятны для слуха? Общая теория эстетики, по-видимому, ненамного продвинулась со времен Пифагора. Итак, одно это открытие греков имеет три аспекта: эксперимент, математические соотношения и эстетику. Физики пока добились успеха только в первых двух. В этой главе мы расскажем о современном понимании открытия Пифагора.
Среди звуков, которые мы слышим, есть такой сорт, который называется шумом. Ему соответствуют какие-то нерегулярные колебания барабанной перепонки уха, вызванные нерегулярными колебаниями находящихся поблизости объектов. Если начертить диаграмму зависимости давления воздуха на барабанную перепонку (а следовательно, и перемещения ее) от времени, то график, соответствующий шуму, будет выглядеть так, как это изображено на фиг. 50.1,а.
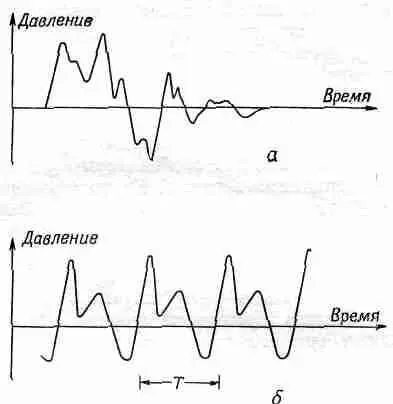
Фиг. 50.1. Давление как функция времени.
а — для шума; б — для музыкального звука.
(Такой шум может например, вызвать топанье ногой.) А музыкальный звук имеет другой характер. Музыка характеризуется наличием более или менее длительных тонов, или музыкальных «нот». (Кстати, музыкальные инструменты тоже умеют производить шум!)
Тон может длиться сравнительно недолго, например когда мы ударяем по клавише фортепьяно, или неопределенно долго, когда, скажем, флейтист берет длинную ноту.
В чем состоит особенность музыкальной ноты с точки зрения давления воздуха? Музыкальный звук отличается от шума тем, что график его периодичен. Форма колебаний давления воздуха со временем пусть даже какая-то неправильная, но она должна повторяться снова и снова. Пример зависимости давления от времени для музыкального звука показан на приведенной выше фиг. 50.1.б.
Обычно музыканты, говоря о музыкальном тоне, определяют три его характеристики — громкость, высоту и «качество». «Громкость», как известно, определяется величиной изменения давления. «Высоте» соответствует период времени повторения основной формы давления («низкие» ноты имеют более длинный период, нежели «высокие»). А под «качеством» тона понимается разница, которую мы способны уловить между двумя нотами одинаковой громкости и высоты. Мы прекрасно различаем звучание гобоя, скрипки или сопрано, даже если высота издаваемых ими звуков кажется одинаковой. Здесь уже дело идет о структуре периодически повторяющейся формы.
Давайте кратко рассмотрим звук, производимый вибрирующей струной.
Если оттянуть струну, а затем отпустить ее, то последующее движение будет определяться волнами, которые мы возбудили. Эти волны, как вы знаете, пойдут в обоих направлениях по струне, а затем отразятся от ее концов. Так они будут бегать взад и вперед довольно долго. И сколь бы сложны ни были эти волны, они будут повторяться периодически снова и снова.
Период этих повторений равен просто времени T, которое требуется волне, чтобы пробежать дважды всю длину струны. Ведь это как раз то время, которое необходимо для того, чтобы любая волна, отразившись от каждого конца, вернулась в начальное положение и продолжала движение в первоначальном направлении. Время, необходимое для того, чтобы волна достигла конца струны в любом направлении, одинаково. Каждая точка струны после целого периода возвращается в свое исходное положение, затем опять отклоняется от него и снова, спустя период, возвращается, и т. д.
Возникающий при этом звук тоже должен повторять те же колебания; вот почему мы, тронув струну, получаем музыкальный звук.
§ 2. Ряд Фурье
В предыдущей главе мы познакомились с другой точкой зрения на колеблющуюся систему. Мы видели, что в струне возникают различные собственные гармоники и что любое частное колебание, которое только возможно получить из начальных условий, можно рассматривать как составленную в надлежащей пропорции комбинацию нескольких одновременно осциллирующих собственных гармоник. Для струны мы нашли, что собственные гармоники имеют частоты w 0, 2w 0, Зw 0, .... Поэтому наиболее общее движение струны складывается из синусоидальных колебаний основной частоты w 0, затем второй гармоники 2w 0, затем третьей гармоники Зw 0и т. д. Основная гармоника повторяется через каждый период T 1=2p/w 0, вторая гармоника — через каждый период T 2=2p/2w 0; она повторяется также и через каждый период Т 1 =2Т 2 , т. е. после двух своих периодов. Точно таким же образом через период Т 1 повторяется и третья гармоника. В этом отрезке укладываются три ее периода. И снова мы понимаем, почему задетая струна через период t 1 полностью повторяет форму своего движения. Так получается музыкальный звук.
До сих пор мы говорили о движении струны. Однако звук, который представляет собой движение воздуха, вызванное движением струны, тоже должен состоять из тех же гармоник, хотя здесь мы уже не можем говорить о собственных гармониках воздуха. К тому же относительная сила различных гармоник в воздухе может быть совсем другой, чем в струне, особенно если струна «связана» с воздухом посредством «звучащей доски». Разные гармоники по-разному связаны с воздухом.
Если для музыкального тона функция f(t) представляет давление воздуха в зависимости от времени (скажем, такая, как на фиг. 50.1.б), то можно ожидать, что f(t) записывается в виде суммы некоторого числа простых гармонических функций от времени (подобных cosw t) для каждой из различных гармонических частот. Если период колебаний равен Т, то основная угловая частота будет w =2 p /Т, а следующие гармоники будут 2w, Зw и т. д.
Здесь появляется небольшое усложнение. Мы не вправе ожидать, что для каждой частоты начальные фазы обязательно будут равны друг другу. Поэтому нужно пользоваться функциями типа cos(wt+j). Вместо этого, однако, проще использовать для каждой частоты как синус, так и косинус. Напомним, что
cos w t+ j)=cosjcosw t- sinjsinw t, (50.1)
а поскольку j — постоянная, то любые синусоидальные колебания с частотой w могут быть записаны в виде суммы членов, в один из которых входит sinwt, а в другой — cos w t.
Итак, мы приходим к заключению, что любая периодическая функция f(t) с периодом Т математически может быть записана в виде
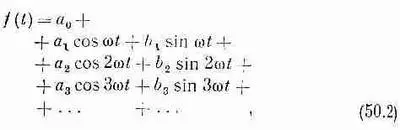
Интервал:
Закладка:



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/1068056/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov.webp)

