Ричард Фейнман - 4a. Кинетика. Теплота. Звук

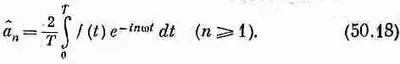
Итак, теперь мы умеем раскладывать периодическую волну на ее гармонические компоненты. Эта процедура называется разложением в ряд Фурье, а отдельные члены называются фурье-компонентами. Однако до сих пор мы не показали, что, определив все фурье-компоненты и затем сложив их, мы дейст­вительно придем назад к нашей функции f(t). Математики до­казали, что для широкого класса функций (в сущности, для всех функций, интересных физикам), которые можно проин­тегрировать, мы снова получаем f(t). Но есть одно небольшое исключение. Если функция f(t) разрывна, т. е. если она неожи­данно прыгает от одного значения к другому, сумма Фурье такой функции даст в точке разрыва значение, лежащее посре­дине между верхним и нижним значениями. Таким образом, если у нас есть странная функция f(t)=0 для 0≤t 0 и f(t)=1 для t 0 ≤t≤T, то ее сумма Фурье всюду даст нам правильную величину, за исключением точки t 0 , где вместо единицы полу­чится 1 / 2 . Во всяком случае, физически даже нельзя требовать, чтобы функция была всюду нулем вплоть до точки t 0 , а в самой точке t 0 вдруг стала равной единице. Может быть, стоило бы спе­циально для физиков издать такой «указ», что любая разрывная функция (которая может быть только упрощением настоящей физической функции) в точке разрыва должна принимать сред­нее значение. Тогда любая такая функция, с любым конечным числом «ступенек», как и все другие интересные для физики функции, будет правильно описываться рядом Фурье.

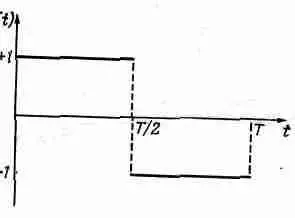
В качестве упражнения предлагаем читателю найти ряд Фурье для функции, показанной на фиг. 50.3.

Фиг. 50.3. Ступенчатая фун­кция. f(t)=+1 для 0

f(t)=-1 для T/2

Поскольку эту функцию нельзя записать в точной алгебраической форме, то брать интеграл от 0 до Т обычным способом невозможно. Однако если разделить его на две части: по интервалу от 0 до T/2 [на котором функция f(t)=1] и по интервалу от T/2 до T [на ко­тором f(t) - 1], то интеграл легко берется. В результате должно получиться

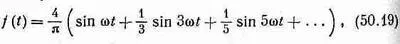
где w=2p/T. Таким образом, оказывается, что для нашей сту­пенчатой волны (со специально выбранной фазой) будут только нечетные гармоники, причем их амплитуды обратно пропор­циональны частотам.

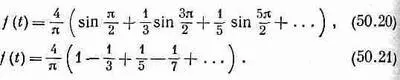
Давайте проверим, что для некоторого значения t результат (50.19) действительно дает снова f(t). Возьмем f = T/4или wt=p/2. Тогда

Сумма этого ряда равна p/4, а, стало быть, f(T)=1 .

§ 5. Теорема об энергии

Энергия волны пропорциональна квадрату ее амплитуды.

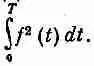
Для сложной волны энергия за один период пропорциональна m

Эту энергию можно связать с коэффициентами Фурье.

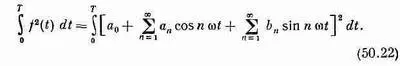
Напишем

После раскрытия квадрата в правой части мы получим сумму всевозможных перекрестных членов типа a 5cos5wtb 7cos7wt. Однако выше мы уже показали [уравнения (50.11) и (50.12)], что интегралы от всех таких членов по одному периоду равны нулю, так что останутся только квадратные члены, подобные a 2 5 cos 2 5wt. Интеграл от любого квадрата косинуса или синуса по одному периоду равен Т/2, так что получаем

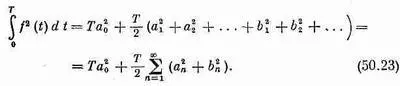
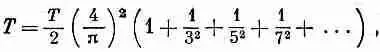
Это уравнение называют «теоремой об энергии», которая гово­рит, что полная энергия волны равна просто сумме энергий всех ее фурье-компонент. Применяя, например, эту теорему к ряду (50.19), мы получаем

поскольку [ f(t) ] 2 = 1 . Таким образом мы узнали, что сумма квад­ратов обратных нечетных чисел равна p 2 /8. Точно так же, выпи­сав сначала ряд Фурье для функции и используя затем теорему об энергии, можно доказать результат, понадобившийся нам в гл. 45, т. е. что 1+ 1/2 4+ 1/3 4+... равно p 4/90.

§ 6. Нелинейная реакция

Наконец, в теории гармоник есть одно очень важное явление, которое необходимо отметить, учитывая его практическую важ­ность, но это уже относится к области нелинейных эффектов. Во всех рассмотренных нами до сих пор системах все предпола­галось линейным; реакция на действие силы, например пере­мещение или ускорение, всегда была пропорциональна силам. Токи в электрической цепи были тоже пропорциональны на­пряжениям и т. д. Теперь мы хотим рассмотреть случаи, когда строгая пропорциональность отсутствует. Представим на ми­нуту устройство, реакция которого x выход=x выхв момент t опре­деляется внешним воздействием x вход= x вхв тот же момент t.

Например, x вхможет быть силой, а х вых— перемещением, или х вх — ток, а x вых— напряжение. Если бы устройство было ли­нейное, то мы бы получили

x вых (t)=Kx вх (t), (50.24)

где К — постоянная, не зависящая ни от t, ни от х ек . Предполо­жим, однако, что устройство только приблизительно линейное, т. е. на самом деле нужно писать

x вых(t)=K[x вх(t)+ex 2 вх(t)]. (50.25)

где e мало по сравнению с единицей. Такие линейная и нелиней­ная реакции показаны на фиг. 50.4.

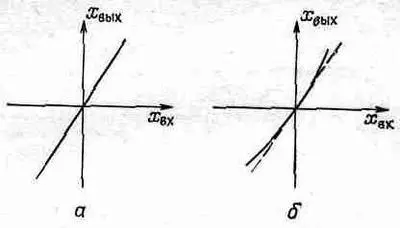
Фиг. 50.4. Реакции, а — линейная,

x вых =kx вх ; б—нелинейная, x вых =k(х вх +ex 2 вх ).

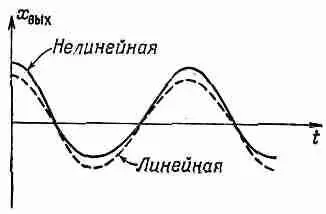
Нелинейная реакция приводит к нескольким важным прак­тическим следствиям. Некоторые из них мы сейчас обсудим. Посмотрим сначала, что получается, если пропустить через по­добное устройство «чистый» тон. Пусть x вх =cos w t. Если мы по­строим график зависимости x выхот времени, то получим сплош­ную кривую, показанную на фиг. 50.5.

Фиг. 50.5. Реакция нелинейного устройства на входящий сигнал cosw t.

Для сравнения показана линейная реак­ция.

Для сравнения там же проведена пунктирная кривая, представляющая реакцию ли­нейной системы. Мы видим, что на выходе получается уже не косинусообразная функция. Она более острая в вершине и более плоская в основании. Поэтому мы говорим, что выходной сигнал искажен. Однако, как известно, такая волна не будет уже чистым тоном, а приобретает какие-то высшие гармоники Можно найти эти гармоники. Подставляя x вх=coswt в уравнение (50.25), получаем