Ричард Фейнман - 3a. Излучение. Волны. Кванты

Все это выглядит весьма таинственно. И тем таинственней, чем больше об этом думаешь. Идей, объясняющих кривую Р12 как результат сложного движения отдельных электронов через оба отверстия, было сфабриковано немало. Но ни одна из этих попыток не была успешной. Ни одна не смогла выразить Р 12через P 1 и Р 2 .

При этом, как ни странно, математика, связывающая P1 и Р 2 с P 12 , проста до чрезвычайности. Ведь кривая P 12 ничем не отличается от кривой I 12на фиг. 37.2, а последнюю-то полу­чить очень просто. То, что приближается к поглотителю, может быть описано двумя комплексными числами j 1и j 2(это функ­ции от х). Квадрат абсолютной величины j 1дает эффект от од­ного отверстия 1: P 1=|j 1| 2. Эффект, полученный при открытом отверстии 2, точно таким же образом получается из j 2, т. е. Р 2=|j 21 2. А общее действие обоих отверстий выразится в виде P 12=|j 1+j 2| 2. Выкладки абсолютно те же, что и для волн на воде! (А попробуйте-ка, кстати, получить такой простой резуль­тат, считая, что электроны шныряют взад и вперед сквозь пластинку по необычным траекториям.)

В конце концов мы приходим к следующему заключению: электроны приходят порциями, подобно частицам, а вероят­ность прибытия этих порций распределена так же, как и интен­сивность волн. Именно в этом смысле электрон и ведет себя «частично как частица, а частью как волна».

Заметим, кстати, что, имея дело с классическими волнами, мы определили интенсивность как среднее по времени от квад­рата амплитуды волны и применили комплексные числа как математический прием, облегчающий расчеты. Но в квантовой механике амплитуды обязаны представляться комплексными числами. Одной только действительной части амплитуд недостаточно. Пока, впрочем, это выглядит лишь как техническая подробность, потому что формулы с виду одни и те же.

А поскольку вероятность прохода сквозь оба отверстия вы­ражается столь просто (хотя и не равна сумме P 1+Р 2), то больше по этому поводу сказать нечего. Но имеется еще мно­жество тонкостей, связанных с таким поведением природы. Хотелось бы рассказать о некоторых из них. Во-первых, раз число частиц, достигающих определенной точки, не равно числу прохождений сквозь отверстие 1 плюс число прохождений че­рез отверстие 2 (как этого можно было ожидать, основываясь на «Утверждении А»), то, несомненно, «Утверждение А» неверно. Неверно, что электроны проходят либо сквозь отверстие 1, либо сквозь отверстие 2. Но этот вывод можно проверить и иначе.

§ 6. Как проследить за электроном?

Попытаемся проделать такой опыт. В наш электронный при­бор как раз за стенкой между двумя отверстиями поместим сильный источник света (фиг. 37.4). Известно, что электричес­кие заряды рассеивают свет. Поэтому, каким бы путем электрон ни прошел к детектору, он обязательно рассеет немного света в наш глаз, и мы увидим, где он проскочил. Скажем, если он проскользнет сквозь отверстие 2, как это показано на рисунке, то мы увидим, как где-то около точки А что-то блеснуло. Если же он проскочит сквозь верхнее отверстие, то блеснет где-то поблизости от отверстия 1. А если бы случилось так, что свет блеснет сразу в двух местах, потому что электрон разделился пополам, то ... Но лучше приступим к опыту!

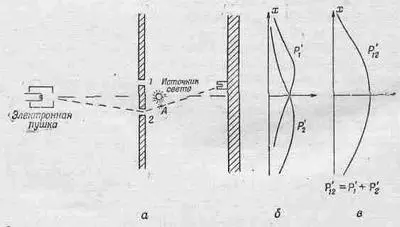
Вот что мы увидим: всякий раз, когда мы слышим из детек­тора «щелк», мы также видим вспышку света или у отверстия 1, или у отверстия 2, но никогда у обоих отверстий сразу! Так происходит при любом положении детектора. Отсюда мы делаем вывод, что когда мы смотрим на электрон, то обнаруживаем, что он проходит или через одно отверстие, или через другое.

Фиг. 37.4. Другой опыт с электронами.

«Утверждение А», как показывает эксперимент, выполняется с необходимостью.

Что же в таком случае неверно в наших доводах против правильности «Утверждения А»? Почему же все-таки P 12 не равно P 1+Р 2? Продолжим наш опыт! Давайте проследим за электронами и посмотрим, что они поделывают. Для каж­дого положения детектора (для каждого фиксированного х) мы подсчитаем, сколько электронов в него попало, и одновременно проследим (наблюдая вспышки), через какие отверстия они прошли. Следить мы будем так: услышав «щелк», мы поставим палочку в первом столбце, если заметим вспышку у первого отверстия; если же вспышка блеснет у отверстия 2, то мы отме­тим это палочкой во второй колонке. Каждый попадающий в детектор электрон будет отнесен к одному из двух классов: либо к классу электронов, проникших сквозь отверстие 1, либо к классу электронов, проникших сквозь отверстие 2. Количество палочек, накопившихся в первой колонке, даст нам р 1— вероятность того, что электрон пройдет к детектору сквозь отверстие 1; точно так же вторая колонка даст Р' 2 — вероят­ность того, что электрон воспользовался отверстием 2. Повторив эти измерения для многих значений х, мы получим кривые р' 1 и Р' 2, показанные на фиг. 37.4,б.

Ну что ж, ничего неожиданного в них нет! Кривая P' 1вышла похожей на кривую P 1,которая получалась, когда от­верстие 2 закрывали, а кривая P' 2похожа на то, что мы полу­чали, когда закрывали отверстие 1. Итак, никаких блужданий от дырки к дырке не существует. Когда мы следим за электро­нами, то оказывается, что они проникают сквозь стенку со щелями в точности так, как мы ожидали. Закрыты ли отверстия или открыты, все равно те электроны, которые мы видели про­никающими сквозь отверстие 1, распределены одинаково.

Но погодите! Какова же теперь полная вероятность — ве­роятность того, что электрон попал в детектор любым путем? У нас уже есть сведения об этом. Сделаем вид, что мы не заме­чали световых вспышек, т. е. сложим палочки, стоящие в обеих колонках. Нам нужно только сложить числа. Для вероятности того, что электрон попал в поглотитель, пройдя через любое из отверстий, мы действительно получим Р' 12= P 1 +P 2 . Выходит, что, хоть нам и удалось проследить, через какое от­верстие проходят электроны, никакой прежней интерференцион­ной кривой P 12не вышло, получилась новая кривая Р' 12— кривая без интерференции! А выключите свет — и снова воз­никнет Р 12.

Мы приходим к заключению, что, когда мы смотрим на электроны, распределение их на экране совсем не такое, как тогда, когда на них не смотрят. Уж не от включения ли света меняется ход событий? Должно быть, электроны — вещь очень деликатная; свет, рассеиваясь на электронах, толкает их и меняет их движение. Мы ведь знаем, что электрическое поле, дей­ствуя на заряд, прилагает к нему силу. От этого, по-видимому, и следует ожидать изменения движения. Во всяком случае, свет оказывает на электроны большое влияние. Пытаясь «проследить» за электронами, мы изменили их движение. Толчки, испыты­ваемые электронами при рассеянии фотонов, очевидно, таковы, что движение электронов сильно изменяется: электрон, который прежде мог попасть в максимум P 12 , теперь приземляется в ми­нимуме Р 12; вот поэтому никакой интерференции и не заметно.