Ричард Фейнман - 3a. Излучение. Волны. Кванты

· · ·

Если движение всего вещества, подобно электронам, нужно описывать, пользуясь волновыми понятиями, то как быть с пулями в нашем первом опыте?

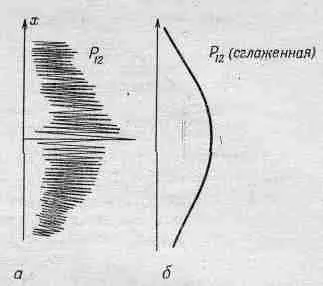
Фиг. 37.5. Интерференционная картина при рассеянии пуль.

а — истинная (схематично); б — на­блюдаемая.

Почему мы не увидели там интерференционной картины? Дело оказывается в том, что у пуль длина волны столь незначительна, что интерференцион­ные полосы становятся очень тонкими. Столь тонкими, что никакой детектор разумных размеров не разделит их на отдель­ные максимумы и минимумы. Мы с вами видели только нечто усредненное — это и есть классическая кривая. На фиг. 37.5 мы попытались схематически изобразить, что происходит с крупными телами. На фиг. 37.5, а показано распределение ве­роятностей для пуль, предсказываемое квантовой механикой. Предполагается, что резкие колебания должны дать представ­ление об интерференционной картине от очень коротких волн. Но любой физический детектор неизбежно вынужден будет накрыть сразу множество зигзагов этой кривой, так что изме­рения, проведенные с его помощью, дадут плавную кривую, показанную на фиг. 37.5,6.

§ 7. Начальные принципы квантовой мвханики

Теперь подытожим основные выводы из наших опытов. Сделаем мы это в такой форме, чтобы они оказались справедли­выми для всего класса подобных опытов. Сводку итогов можно записать проще, если сперва определить «идеальный опыт», т. е. опыт, в котором отсутствуют неопределенные внешние влияния и нет никаких не поддающихся учету изменений, колебаний и т. д. Точная формулировка будет такова: «Идеаль­ным опытом называется такой, в котором все начальные и ко­нечные условия опыта полностью определены». Такую сово­купность начальных и конечных условий мы будем называть «событием». (Например: «электрон вылетает из пушки, попада­ет в детектор, и больше ничего не происходит».) А сейчас дадим нашу сводку выводов.

СВОДКА ВЫВОДОВ

Вероятность события в идеальном опыте дается квадра­том абсолютной величины комплексного числа j, назы­ваемого амплитудой вероятности.

Р — вероятность,

j — амплитуда вероятности, (37 6)

Р=|j| 2.

Если событие может произойти несколькими взаимно исключающими способами, то амплитуда вероятности со­бытия — это сумма амплитуд вероятностей каждого отдель­ного способа. Возникает интерференция.

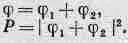
(37.7)

3) Если ставится опыт, позволяющий узнать, какой из этих взаимно исключающих способов на самом деле осуще­ствляется, то вероятность события—это сумма вероятно­стей каждого отдельного способа. Интерференция отсут­ствует.

P = P 1+P 2(37.8)

· · ·

Быть может, вам все еще хочется выяснить: «А почему это? Какой механизм прячется за этим законом?» Так вот: никому никакого механизма отыскать не удалось. Никто в мире не смо­жет вам «объяснить» ни на капельку больше того, что «объяс­нили» мы. Никто не даст вам никакого более глубокого представ­ления о положении вещей. У нас их нет, нет представлений о более фундаментальной механике, из которой можно вывести эти результаты.

Мы хотели бы подчеркнуть очень важное различие между классической и квантовой механикой. Мы уже говорили о веро­ятности того, что электрон попадает туда-то и туда-то в данных обстоятельствах. Мы подразумевали, что с нашим (да и с са­мым лучшим) экспериментальным устройством невозможно бу­дет предсказывать точно, что произойдет. Мы способны только определять шансы! Это означало бы, если это утверждение пра­вильно, что физика отказалась от попыток предсказывать точно, что произойдет в определенных условиях. Да! Физика и впрямь сдалась. Мы не умеем предсказывать, что должно было бы случиться в данных обстоятельствах. Мало того, мы уверены, что это немыслимо: единственное, что поддается предвычислению,— это вероятность различных событий. Прихо­дится признать, что мы изменили нашим прежним идеалам понимания природы. Может быть, это шаг назад, но никто не научил нас, как избежать его!

Сделаем теперь несколько замечаний об одном утвержде­нии, которое иногда делали те, кто не хотел пользоваться приведенным описанием. Они говорили: «Может быть, в электроне происходят какие-то внутренние процессы, имеются какие-то внутренние переменные, о чем мы пока ничего не знаем. Может быть, именно поэтому мы не умеем предугадывать, что случит­ся. А если бы мы могли попристальней вглядеться в электрон, то смогли бы сказать, куда он придет». Насколько нам извест­но, такой возможности нет. Трудности все равно остаются. Предположим, что внутри электрона есть механизм какого-то рода, определяющий, куда электрон собирается попасть. Тогда эта машина должна определить также, через какое от­верстие он намерен проследовать. Но не забывайте, что вся эта внутриэлектронная механика не должна зависеть от того, что делаем мы, и, в частности, от того, открыли мы данное отверстие или нет. Значит, если электрон, отправляясь в путь, уже прикинул, сквозь какую дырку он протиснется и где он приземлится, то для электронов, облюбовавших отверстие 1, мы получим распределение P 1, а для остальных — распреде­ление p2. А тогда для тех электронов, которые прошли через оба отверстия, с необходимостью распределение окажется сум­мой P 1 +P 2 . Не видно способа обойти этот вывод. Но мы экспериментально доказали, что он неверен. Никто еще не нашел отгадки этой головоломки. Стало быть, в настоящее время приходится ограничиваться расчетом вероятностей. Мы говорим «в настоящее время», но мы очень серьезно подозре­ваем, что все это — уже навсегда и разгрызть этот орешек че­ловеку не по зубам, ибо такова природа вещей.

§ 8. Принцип неопределенности

Вот как сам Гейзенберг сформулировал свой принцип не­определенности: если вы изучаете какое-то тело и вы в состоянии определить z-компоненту импульса тела с неопределенностью Dp, то вы не можете одновременно определить координату х тела с точностью, большей чем Dx= h/Dp.

Произведение неопределенностей в положении тела и в его импульсе в любой момент должно быть больше постоянной Планка. Это частный случай принципа неопределенности. Более, общая формулировка была высказана в предыдущем параг­рафе: нельзя никаким образом устроить прибор, определяю­щий, какое из двух взаимно исключающих событий осуществилось, без того, чтобы в то же время не разрушилась интерфе­ренционная картина.

Сейчас на одном частном случае мы покажем, что, если не иметь в своем распоряжении какого-нибудь принципа, наподо­бие принципа Гейзенберга, трудностей избежать никак нельзя. Представим себе такое видоизменение опыта, показанного на фиг. 37.3, в котором стенкой с отверстиями служит пластинка на катках, способная откатываться вверх и вниз (в x-направлении),