Ричард Фейнман - 3a. Излучение. Волны. Кванты

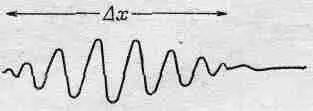
Фиг. 38.1. Волновой пакет длиной Dx.

Выходит, что амплитуда описывает цуг волн протяженностью Dx (фиг. 38.1), а длине волны (расстоянию между горбами волн) в цуге волн соответствует некоторое значение импульса час­тицы.

Здесь мы сталкиваемся со странным и в то же время очень простым явлением, никак непосредственно с квантовой меха­никой не связанным. Оно известно всем, кто занимался волна­ми, даже не зная квантовой механики, а именно: нельзя одно­значно определить длину волны для короткого цуга волн. У такого цуга нет определенной длины волн; в волновом числе имеется неопределенность, связанная с конечной длиной цуга, а значит, и неопределенность в импульсе.

§ 2. Измерение положения и импульса

Чтобы понять, почему в квантовой механике появляется неопределенность в положении и (или) в импульсе, рассмотрим два примера. Мы уже видели раньше, что если бы этого не было, если бы можно было параллельно измерять и местонахождение, и импульс какого-то тела, то возник бы парадокс. К счастью, парадокса не возникает, а то обстоятельство, что неопределен­ность естественным образом вытекает из волновой картины, свидетельствует, что все здесь взаимосвязано.

Вот первый пример, показывающий связь импульса и коор­динаты в условиях, которые легко себе представить. Пусть сквозь единственную щель в экране проникают частицы, при­шедшие издалека и обладающие определенной энергией. Дви­жутся все они горизонтально (фиг. 38.2). Сосредоточим наше внимание на вертикальной составляющей импульса. У каждой из этих частиц имеется (в обычном классическом смысле) го­ризонтальная составляющая импульса определенной величины р 0 . Вертикальная составляющая импульса р y (до того, как частица пройдет сквозь прорезь) также в классическом смысле хорошо известна: частицы не движутся ни вверх, ни вниз, по­тому что их источник очень удален, значит, вертикальная со­ставляющая импульса частицы в точности равна нулю. А теперь предположим, что ширина щели равна В.

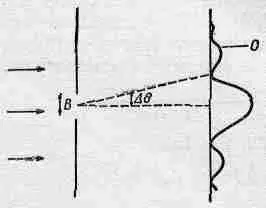
Фиг. 38.2. Дифракция частиц, проходящих сквозь щель.

Когда частица прой­дет через щель, то ее вертикальная координата у определится с хорошей точностью ± В. Это значит, что неопределенность в положении частицы Dy будет порядка В. Может, вы захотите сказать, что Dp y=0, потому что импульс частиц, мол, точно горизонтален? Но это не так. Это прежде мы знали, что импульс имеет только горизонтальную составляющую, а теперь мы этого уже не знаем. Перед тем как частица проникла сквозь щель, мы не знали ее вертикальной координаты. После того как час­тица проникла сквозь щель, мы узнали ее вертикальную коор­динату, но потеряли информацию об ее вертикальной состав­ляющей импульса! Почему? Да потому, что, согласно волновой теории, происходит отклонение, или дифракция, волн, проник­ших сквозь щель, подобно тому как это бывает со светом. По­этому есть конечная вероятность того, что частицы, пройдя сквозь щель, не пойдут прямо вперед. Вся картина распростра­нения расплывается за счет дифракции, и угол этого расшире­ния (угол, под которым виден первый минимум) есть мера неоп­ределенности направления частицы.

Каким образом происходит расплывание изображения в ширину? Расплывание означает, что существует некая вероят­ность того, что частица отправится вверх или вниз, т. е. приоб­ретет компоненту импульса, направленную вверх или вниз. (Мы говорим и о вероятности и о частице, потому что дифрак­ционную картину можно обнаружить с помощью счет­чика частиц, а когда счетчик регистрирует частицу, скажем, в точке С на фиг. 38.2, то он регистрирует частицу целиком. А это значит в классическом смысле, что частица имеет вертикальный импульс, направляющий ее из щели прямо в точку С.)

Чтобы примерно представить себе степень расплывания импульса, напишем, что вертикальный импульс р у размазан на р 0Dq, где р 0— горизонтальный импульс. Чему же равно Dq в размазанной картине? Известно, что первый минимум на­блюдается при угле Dq таком, что в этом направлении волна от дальнего края щели должна отстать на одну свою длину от волны от ближнего края (мы об этом уже говорили в гл. 30). Стало быть, Dq равно l/B, и тем самым Dp yв этом эксперименте равно р 0 l /В. Чем меньше будет В, чем точнее будет определять­ся положение частицы, тем шире будет дифракционная картина. Вспомните, что когда мы закрывали щели в эксперименте с микроволнами, то интенсивность в стороне от щели возрастала. Значит, чем уже щель, тем шире становится картина дифрак­ции, тем правдоподобнее, что мы обнаружим у частицы импульс, направленный в сторону. И неопределенность в вертикальном импульсе, действительно, обратно пропорциональна неопре­деленности в у, потому что их произведение равно p 0l .

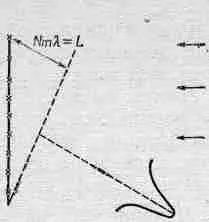
Фиг. 38.3. Определение импульса с помощью дифракционной решет­ки.

Но l — это длина волны, а р 0— импульс, и в соответствии с квантовой механикой их произведение — это постоянная Планка h. Получается, что произведение неопределенностей в вертикальном импульсе и в вертикальной координате есть величина порядка h:

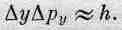
(38.3)

Мы не можем приготовить систему, в которой положение час­тицы по вертикали было бы известно, и в то же время предска­зывать с определенностью, превышающей h/Dy, насколько ее движение отклонится от вертикали. Неопределенность в вер­тикальном импульсе всегда больше h/Dy, если Dy — неопре­деленность, с какой мы знаем положение частицы.

Некоторые люди утверждают, что в квантовой механике все неправильно. Когда, говорят они, частица приближалась сле­ва, ее вертикальный импульс был равен нулю. А когда она прошла через щель, стало известно ее положение. И то, и дру­гое может быть определено с любой точностью.

Совершенно верно. Мы можем зарегистрировать частицу и определить, каково ее положение и каким должен был быть ее импульс, чтобы она попала туда, куда она попала. Это все верно. Но соотношение неопределенностей (38.3) ничего общего с этим не имеет. Уравнение (38.3) относится к возмож­ности предсказания, а не к замечаниям о том, что произошло в прошлом. Какая польза в том, что мы скажем: «Я знал, каков был импульс до прохода частицы сквозь щель, а теперь узнал к тому же и координату»? Ведь теперь-то знание об импульсе частицы уже утеряно. Раз она прошла сквозь щель, то мы уже не можем больше предсказывать ее вертикальный импульс. Речь идет о теории, способной к предсказаниям, а не об изме­рениях после того, как все завершилось. Мы и обсуждаем воп­рос о том, что можно предвидеть.