Ричард Фейнман - 3. Излучение. Волны. Кванты

(32.4)

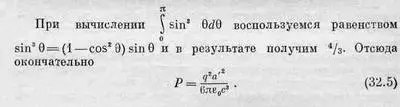
Необходимо сделать несколько замечаний по поводу этого выражения. Прежде всего, поскольку а' есть вектор, то а' 2в формуле (32.5) означает а'·а', т. е. квадрат длины вектора. Во-вторых, в формулу (32.2) для потока входит ускорение, взятое с учетом запаздывания, т. е. ускорение в тот момент времени, когда была излучена энергия, проходящая сейчас через поверхность сферы. Может возникнуть мысль, что энергия действительно была излучена точно в указанный момент вре­мени. Но это не совсем правильно. Момент излучения нельзя определить точно. Можно вычислить результат только такого движения, например колебания и т. п., где ускорение в конце концов исчезает. Следовательно, мы можем найти только полный поток энергии за весь период колебаний, пропорциональный среднему за период квадрату ускорения. Поэтому а' 2в (32.5) должно означать среднее по времени от квадрата ускорения. Для такого движения, когда ускорение в начале и в конце обращается в нуль, полная излученная энергия равна интегралу по времени от выражения (32.5).

Посмотрим, что дает формула (32.5) для осциллирующей системы, для которой ускорение а' имеет вид w 2x 0е i w t. Сред­нее за период от квадрата ускорения равно (при возведении

в квадрат надо помнить, что на самом деле вместо экспоненты должна входить ее действительная часть — косинус, а среднее от cos 2wt дает l/ 2):

(32.6)

Эти формулы были получены сравнительно недавно — в начале XX века. Это замечательные формулы, они имели огромное историческое значение, и о них стоило бы почи­тать в старых книгах по физике. Правда, там использовалась другая система единиц, а не система СИ. Однако в конечных результатах, относящихся к электронам, эти осложнения можно исключить с помощью следующего правила соответствия: вели­чина q 2 e/4pe 0, где q е— заряд электрона (в кулонах), раньше записывалась как е 2. Легко убедиться, что в системе СИ значе­ние е численно равно 1,5188·10 -14, поскольку мы знаем, что

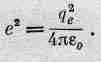
q e= 1,60206·10 -1 9и 1/4pe 0= 8,98748·10 9. В дальнейшем мы будем часто пользоваться удобным обозначением

(32.7)

Если это численное значение e подставить в старые формулы, то все остальные величины в них можно считать опре­деленными в системе СИ. Например, формула (32.5) прежде имела вид Р = 2/ 3е 2а 2/с 3. А потенциальная энергия прото­на и электрона на расстоянии r есть q2e /4pe 0r или е 2/r, где е =1,5188-10 - 14ед. СИ.

§ 3. Радиационное затухание

Заряд, закрепленный на пружине с собственной частотой w 0(или электрон в атоме), даже в абсолютно пустом простран­стве не сможет колебаться бесконечно долго, поскольку, колеб­лясь, он теряет энергию на излучение. Никаких сил сопротив­ления в обычном смысле этого слова, никакой вязкости здесь нет. Но колебания не будут происходить «вечно», вследствие излучения они будут медленно замирать. А насколько медленно? Определим для осциллятора величину Q, вызванную так назы­ваемым радиационным сопротивлением или радиационным зату­ханием. Для любой колеблющейся системы величина Q равна энергии системы в данный момент времени, деленной на потери энергии, отнесенные к 1 рад:

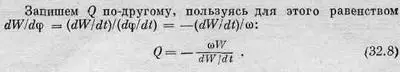
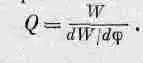
Если Q задано, то легко получить закон спадания энергии колебаний: dW/dt = (-w/Q)W, откуда следует W =W 0e - w t / Q; здесь W 0— начальная энергия (при t = 0).

Чтобы найти Q для излучающего осциллятора, вернемся к формуле (32.8) и подставим вместо dW/dt выражение (32.6).

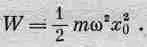
А что нужно взять в качестве энергии W осциллятора? Кине­тическая энергия осциллятора равна 1/2mv 2, а средняя кинети­ческая энергия равна mш 2x20/4. Но мы помним, что полная энер­гия осциллятора равна средней кинетической плюс средняя потенциальная, причем обе они для осциллятора равны; поэтому полная энергия равна

(32.9)

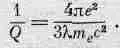
Какую частоту следует подставить в наши формулы? Мы возь­мем собственную частоту w 0, потому что практически это и есть частота излучения атома, а вместо m подставим m e . После ряда сокращений эта формула приводится к виду

(32.10)

(Для большей ясности и из соображений близости к исторически принятой форме мы ввели величину е 2= q 2 e/4pe 0и записали 2p/l вместо w 0/с.) Поскольку величина Q безразмерна, множи­тель е 2/m ес 2, зависящий только от массы и заряда электрона и выражающий его внутренние свойства, обязан иметь размер­ность длины. Он был назван классическим радиусом электрона, потому что в старых моделях электрона радиационное сопротив­ление пытались объяснить действием одной части электрона на другие его части, для чего размеры электрона приходилось вы­бирать порядка e 2/m ec 2. Но эта величина потеряла свой прежний смысл, и никто теперь не считает, что электрон имеет такой

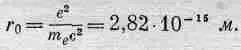
радиус. Численное значение классического радиуса электрона следующее:

(32.11)

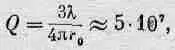
Вычислим теперь значение Q для атома, излучающего ви­димый свет, например для атома натрия. Длина волны излу­чения натрия равна примерно 6000 Е и находится в желтой части спектра; эта величина довольно типична. Отсюда

(32.12)

т. е. для атомов Q порядка 10 8. Это значит, что атомный осциллятор колеблется 10 8 рад, или примерно 10 7периодов, прежде чем его энергия уменьшится в 1 /е раз. Частота колебаний света v = с/l при длине волны 6000 Е составляет 10 15 гц, а, следовательно, время жизни, т. е. время, за которое энер­гия уменьшится в Не раз, есть величина порядка 10 -8сек.

Примерно за такое же время высвечиваются свободные атомы в обычных условиях. Проведенная оценка справедлива только для атомов в пустом пространстве, не подверженных никаким внешним воздействиям. Если электрон находится в твердом теле, он сталкивается с другими атомами и электро­нами, и тогда возникает добавочное сопротивление и затухание будет другим.