Ричард Фейнман - 3. Излучение. Волны. Кванты

Сам факт зависимости показателя преломления от частоты называется дисперсией, так как именно из-за дисперсии свет «диспергирует», раскладывается призмой в спектр. Формула, выражающая показатель преломления как функцию частоты, называется формулой дисперсии. Итак, мы нашли дисперсион­ную формулу. (За последние несколько лет «дисперсионные фор­мулы» стали использоваться в теории элементарных частиц.)

Наша дисперсионная формула предсказывает ряд новых инте­ресных эффектов. Если частота w 0лежит в области видимого света или если измерять показатель преломления вещества, например стекла, для ультрафиолетовых лучей (где w близко к w 0), то знаменатель стремится к нулю, а показатель преломления становится очень большим. Пусть, далее, w больше w 0. Такой случай возникает, например, если облучать вещества типа стекла рентгеновскими лучами. Кроме того, многие вещества, непро­зрачные для обычного света (скажем, уголь), прозрачны для рентгеновских лучей, поэтому можно говорить о показателе преломления этих веществ для рентгеновских лучей. Собствен­ные частоты атомов углерода гораздо меньше частоты рентгенов­ских лучей. Показатель преломления в этом случае дается нашей дисперсионной формулой, если положить w 0=0 (т. е. мы прене­брегаем w 0 2по сравнению с w 2).

Аналогичный результат получается при облучении газа сво­бодных электронов радиоволнами (или светом). В верхних слоях атмосферы ультрафиолетовое излучение Солнца выбивает элек­троны из атомов, в результате чего образуется газ свободных электронов. Для свободных электронов w 0=0 (упругой возвращающей силы нет). Полагая в нашей дисперсионной формуле w 0=0, получаем разумную формулу для показателя преломления радиоволн в стратосфере, где N теперь означает плотность сво­бодных электронов (число на единицу объема) в стратосфере. Но, как видно из формулы, при облучении вещества рентгеновскими лучами или электронного газа радиоволнами член (ш02-ш 2) ста­новится отрицательным, откуда следует, что n меньше единицы. Это значит, что эффективная скорость электромагнитных волн в веществе больше c! Может ли так быть?

Может. Хотя мы и говорили, что сигналы не могут распро­страняться быстрее скорости света, тем не менее показатель преломления при некоторой частоте может быть как больше, так и меньше единицы. Это просто означает, что сдвиг фазы за счет рассеяния света либо положителен, либо отрицателен. Кроме того, можно показать, что скорость сигнала определяется показателем преломления не при одном значении частоты, а при многих частотах. Показатель преломления указывает на ско­рость движения гребня волны. Но гребень волны не составляет еще сигнала. Чистая волна без всяких модуляций, т. е. состоя­щая из бесконечно повторяющихся правильных осцилляции, не имеет «начала», и ее нельзя использовать для посылки сигна­лов времени. Чтобы послать сигнал, волну нужно видоизменить, сделать на ней отметку, т. е. сделать ее кое-где потолще или по­тоньше. Тогда волна будет содержать не одну частоту, а целый ряд частот, и можно показать, что скорость распространения сигнала зависит не от одного значения показателя преломления, а от характера изменения показателя с частотой. Мы пока от­ложим этот вопрос. В гл. 48 (вып. 4) мы вычислим скорость рас­пространения сигналов в стекле и убедимся, что она не превышает скорости света, хотя гребни волны (понятия чисто математиче­ские) движутся быстрее скорости света.

Несколько слов по поводу механизма этого явления. Главная трудность здесь связана с тем фактом, что вынужденное движе­ние зарядов противоположно по знаку направлению поля. Дей­ствительно, в выражении (31.16) для смещения заряда х множи­тель (w 0-w 2) отрицателен для малых w 0и смещение имеет обратный знак по отношению к внешнему полю. Получается, что, когда поле действует с некоторой силой в одном направлении, заряд движется в противоположном направлении.

Как случилось, что заряд стал двигаться в сторону, проти­воположную силе? В самом деле, при включении поля заряд движется не противоположно силе. Сразу после включения поля возникает переходный режим, затем колебания устанавливаются и только после этого колебания заряды направлены про­тивоположно внешнему полю. Одновременно результирующее поле начинает опережать по фазе поле источника. Когда мы го­ворим, что «фазовая скорость», или скорость гребней волны, больше с, то мы имеем в виду именно опережение по фазе.

На фиг. 31.4 показан примерный вид волн, возникающих при резком включении волны источника (т. е. при посылке сигнала).

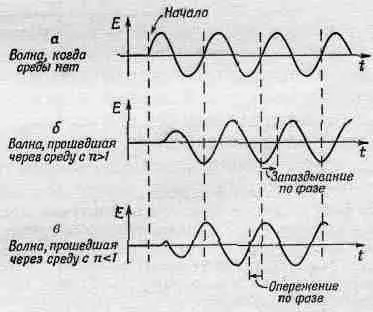
Фиг. 31.4. Волновые «сигналы».

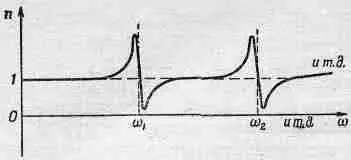
Фиг. 31.5. Показатель преломления как функция частоты.

Из рисунка видно, что для волны, проходящей в среде с опере­жением по фазе, сигнал (т. е. начало волны) не опережает по времени сигнал источника.

Обратимся теперь снова к дисперсионной формуле. Следует помнить, что полученный нами результат несколько упрощает истинную картину явления. Чтобы быть точными, в формулу необходимо внести некоторые поправки. Прежде всего, в нашу модель атомного осциллятора следует ввести затухание (иначе осциллятор, раз начав, будет колебаться до бесконечности, что неправдоподобно). Движение затухающего осциллятора мы уже изучали в одной из прошлых глав [см. уравнение (23.8)]. Учет затухания приводит к тому, что в формулах (31.16), а поэтому и

в (31.19), вместо (w 0 2-w 2) появляется (w 0 2-w 2+igw)' где g — коэффициент затухания.

Вторая поправка к нашей формуле возникает потому, что каждый атом обычно имеет несколько резонансных частот. Тогда вместо одного вида осцилляторов, нужно учесть действие не­скольких осцилляторов с разными резонансными частотами, ко­лебания которых происходят независимо друг от друга, и сло­жить вклады от всех осцилляторов.

Пусть в единице объема содержится N kэлектронов с соб­ственной частотой (w kи коэффициентом затухания g k. Наша дисперсионная формула примет в результате вид

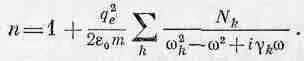
(31.20)

Это окончательное выражение для показателя преломления справедливо для большого числа веществ. Примерный ход показателя преломления с частотой, даваемый формулой (31.20), приведен на фиг. 31.5.

Вы видите, что всюду, за исключением области, где w очень близко к одной из резонансных частот, наклон кривой положи­телен. Такая зависимость носит название «нормальной» диспер­сии (потому что этот случай встречается наиболее часто). Вблизи резонансных частот кривая имеет отрицательный наклон, и в этом случае говорят об «аномальной» дисперсии (имея в виду «ненормальную» дисперсию), потому что она была наблюдена задолго до того, как узнали об электронах, и казалась в то время необычной, С нашей точки зрения, оба наклона вполне «нор­мальны»!