Ричард Фейнман - 3. Излучение. Волны. Кванты

§ 2. Поле, излучаемое средой

Мы должны теперь выяснить, имеет ли поле осциллирующих зарядов в пластинке тот же вид, что и поле Е аво втором члене (31.8). Если это так, то тем самым мы найдем и показатель пре­ломления n [поскольку n — единственный фактор в (31.8), не выражающийся через фундаментальные величины]. Вернемся теперь к вычислению поля Е а , создаваемого зарядами пластин­ки. (Для удобства мы выписали в табл. 31.1 обозначения, которы­ми мы уже пользовались, и те, которые нам понадобятся в дальнейшем.)

Таблица 31.1 ● обозначения которыми мы пользуемся

ПРИ ВЫЧИСЛЕНИИ _______

E s поле, создаваемое источником

Е аполе, создаваемое зарядами пластинки

Dz толщина пластинки

z расстояние по нормали к пластинке

n показатель преломления

w частота (угловая) излучения

N число зарядов в единице объема пластинки

h число зарядов на единицу площади пластинки

q езаряд электрона

m масса электрона

w 0резонансная частота электрона, связанного в атоме

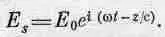
Если источник S (на фиг. 31.1) находится слева на достаточно большом расстоянии, то поле E sимеет одинаковую фазу по всей длине пластинки, и вблизи пластинки его можно записать в виде

(31.9)

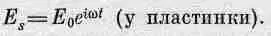
На самой пластинке в точке z=0 мы имеем

(31.10)

Это электрическое поле воздействует на каждый электрон в атоме, и они под действием электрической силы qE будут коле­баться вверх и вниз (если e0 направлено вертикально). Чтобы найти характер движения электронов, представим атомы в виде маленьких осцилляторов, т. е. пусть электроны упруго соеди­нены с атомом; это значит, что смещение электронов из нормаль­ного положения под действием силы пропорционально величине силы.

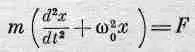
Если вы слышали о модели атома, в которой электроны вращаются по орбите вокруг ядра, то эта модель атома вам покажется просто смешной. Но это лишь упрощенная модель. Точная теория атома, основанная на квантовой механике, утверждает, что в процессах с участием света электроны ведут себя так, как будто они закреплены на пружинах. Итак, предположим, «что на электроны действует линейная возвращающая сила, и поэтому они ведут себя как осцилляторы с массой m и резонансной частотой w 0. Мы уже занимались изучением таких осцилляторов и знаем уравнение движения, которому они под­чиняются:

(31.11)

(здесь F — внешняя сила).

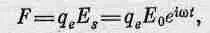
В нашем случае внешняя сила создается электрическим полем волны источника, поэтому можно написать

(31.12)

где q e— заряд электрона, а в качестве E Sмы взяли значение Е S= Е 0е i w tиз уравнения (31.10). Уравнение движения элект­рона приобретает вид

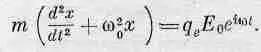
(31.13)

Решение этого уравнения, найденное нами раньше, выглядит следующим образом:

(31.15)

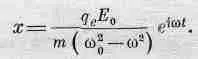
откуда

(31.16)

Мы нашли то, что хотели,— движение электронов в пластинке. Оно одинаково для всех электронов, и только среднее положение («нуль» движения) у каждого электрона свое.

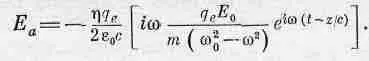
Теперь мы в состоянии определить поле Е а, создаваемое атомами в точке Р, поскольку поле заряженной плоскости было найдено еще раньше (в конце гл. 30). Обращаясь к уравнению (30.19), мы видим, что поле Е ав точке Р есть скорость заряда, за­паздывающая по времени на величину z/c, умноженная на отри­цательную константу. Дифференцируя х из (31.16), получаем скорость и, введя запаздывание [или же просто подставляя х 0из (31.15) в (30.18)], приходим к формуле

(31.17)

Как и следовало ожидать, вынужденное колебание электронов привело к новой волне, распространяющейся вправо (на это указывает множитель ехр[iw(t-z/c)]); амплитуда волны про­порциональна числу атомов на единице площади пластинки (множитель h), а также амплитуде поля источника (Е 0). Кроме того, возникают и другие величины, зависящие от свойств ато­мов (q e , m , w 0).

Самый важный момент, однако, заключается в том, что фор­мула (31.17) для Е aочень похожа на выражение Е ав (31.8), полученное нами с помощью введения запаздывания в среде с показателем преломления n. Оба выражения совпадают, если положить

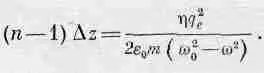
(31.18)

Заметьте, что обе стороны этого равенства пропорциональны Dz, поскольку h — число атомов на единицу площади — равно NDz, где N — число атомов на единицу объема пластинки. Под­ставляя NDz вместо h и сокращая на Dz, получаем наш основ­ной результат — формулу для показателя преломления, выра­женную через константы, зависящие от свойств атомов, и часто­ту света:

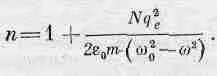
(31.19)

Эта формула «объясняет» показатель преломления, к чему мы и стремились.

§ 3. Дисперсия

Полученный нами результат очень интересен. Он дает не только показатель преломления, выраженный через атомные постоянные, но указывает, как меняется показатель преломления с частотой света w. С помощью простого утверждения «свет дви­жется с меньшей скоростью в прозрачной среде» мы никогда бы не смогли прийти к этому важному свойству. Нужно, конечно, еще знать число атомов в единице объема и собственную частоту атомов w 0. Мы еще не умеем определять эти величины, поскольку они разные для разных материалов, а общую теорию по данному вопросу мы сейчас изложить не можем. Общая теория свойств различных веществ — их собственных частот и

т. п.— форму­лируется на основе квантовой механики. Кроме того, свойства различных материалов и величина показателя преломления сильно меняются от материала к материалу, и поэтому вряд ли можно надеяться, что вообще удастся получить общую форму­лу, пригодную для всех веществ.

Тем не менее попробуем применить нашу формулу к разным средам. Прежде всего, для большинства газов (например, для воздуха, большей части бесцветных газов, водорода, гелия и т. д.) собственные частоты колебаний электронов соответствуют уль­трафиолетовому свету. Эти частоты много больше частот види­мого света, т. е. w 0много больше w, и в первом приближении можно пренебречь w 2по сравнению с w 0 2. Тогда показатель преломления получается почти постоянным. Итак, для газов показатель преломления можно считать константой. Этот вывод справедлив также и для большинства других прозрачных сред, например для стекла. Взглянув более внимательно на наше выражение, можно заметить, что при увеличении со знамена­тель уменьшается, а, следовательно, показатель преломления растет. Таким образом, n медленно увеличивается с ростом час­тоты. Для синего света показатель преломления больше, чем для красного. Именно поэтому синие лучи сильнее отклоняются призмой, чем красные.