Ричард Фейнман - 2a. Пространство. Время. Движение

А производные тоже умножатся на A и поэтому Ах так же хорошо удовлетворит уравнению, как и х. Послушаем, что скажет по этому поводу физик. Если грузик растянет пружинку вдвое больше прежнего, то вдвое возрастет сила, вдвое возрастет ус­корение, в два раза больше прежней будет приобретенная ско­рость и за то же самое время грузик пройдет вдвое большее рас­стояние. Но это вдвое большее расстояние — как раз то самое расстояние, которое надо пройти грузику до положения равно­весия. Таким образом, чтобы достичь равновесия, требуется столько же времени и оно не зависит от начального смещения. Иначе говоря, если движение описывается линейным уравне­нием, то независимо от «силы» оно будет развиваться во вре­мени одинаковым образом.

Ошибка пошла нам на пользу — мы узнали, что, умножив решение на постоянную, мы получим решение прежнего уравне­ния. После нескольких проб и ошибок можно прийти к мысли, что вместо манипуляций с х надо изменить шкалу времени. Иначе говоря, уравнение (21.2) должно иметь решение вида

x=cos w 0t. (21.4)

(Здесь w 0— вовсе не угловая скорость вращающегося тела, но нам не хватит всех алфавитов, если каждую величину обозна­чать особой буквой.) Мы снабдили здесь w индексом 0, потому что нам предстоит встретить еще много всяких омег: запомним, что w 0соответствует естественному движению осциллятора. Попытка использовать (21.4) в качестве решения более успешна, потому что dx/dt=- ( w 0sin w 0t и d 2 x/dt 2 =-w 2 0 w s w 0 t=-w 2 0x. На­конец-то мы решили то уравнение, которое и хотели решить. Это уравнение совпадает с (21.2), если w 2 0 =k/m.

Теперь нужно понять физический смысл w 0. Мы знаем, что косинус «повторяется» после того, как угол изменится на 2я. Поэтому x=cosw 0 t будет периодическим движением; полный цикл этого движения соответствует изменению «угла» на 2p. Величину w 0 t часто называют фазой движения. Чтобы изменить w 0t на 2p , нужно изменить t на t 0 (период полного колебания); конечно, t 0 находится из уравнения w 0 t 0 = 2p. Это значит, что w 0t 0нужно вычислять для одного цикла, и все будет повто­ряться, если увеличить t на t 0 ; в этом случае мы увеличим фазу на 2p. Таким образом,

Значит, чем тяжелее грузик, тем медленнее пружинка будет ко­лебаться взад и вперед. Инерция в этом случае будет больше, и если сила не изменится, то ей понадобится большее время для разгона и торможения груза. Если же взять пружинку пожест­че, то движение должно происходить быстрее; и в самом деле, период уменьшается с увеличением жесткости пружины.

Заметим теперь, что период колебаний массы на пружинке не зависит от того, как колебания начинаются. Для пружинки как будто безразлично, насколько мы ее растянем. Уравнение движения (21.2) определяет период колебаний, но ничего не го­ворит об амплитуде колебания. Амплитуду колебания, конеч­но, определить можно, и мы сейчас займемся этим, но для этого надо задать начальные условия.

Дело в том, что мы еще не нашли самого общего решения уравнения (21.2). Имеется несколько видов решений. Реше­ние x=acosw 0 t соответствует случаю, когда в начальный мо­мент пружинка растянута, а скорость ее равна нулю. Можно иначе заставить пружинку двигаться, например улучить момент, когда уравновешенная пружинка покоится (х=0), и резко ударить по грузику; это будет означать, что в момент t=0 пружинке сообщена какая-то скорость. Такому движению будет соответствовать другое решение (21.2) — косинус нужно заменить на синус. Бросим в косинус еще один камень: если x=cos w 0t—решение, то, войдя в комнату, где качается пружин­ка, в тот момент (назовем его «t=0»), когда грузик проходит через положение равновесия (x=0), мы будем вынуждены заме­нить это решение другим. Следовательно, x=cosw 0 t не может быть общим решением; общее решение должно допускать, так сказать, перемещение начала отсчета времени. Таким свойст­вом обладает, например, решение x=acosw 0 (t-t 1 ), где t 1— какая-то постоянная. Далее, можно разложить

cos(w 0 t+D )=cos w 0 t cos D -sin w 0 t sin D и записать

x=A cos w 0 t + В sin w 0 t ,

где A=acos D и В=- asin D . Каждую из этих форм можно ис­пользовать для записи общего решения (21.2): любое из су­ществующих в мире решений дифференциального уравнения

d 2 x/dt 2 =-w 2 0 x можно записать в виде

x=acosw 0 (t-t 1 ), (21.6а)

или

x=acos ( w 0 t+D ), (21.6б)

или

х=A cos w 0 t+B sin w 0 t. (21.6в)

Некоторые из встречающихся в (21.6) величин имеют наз­вания: w 0называют угловой частотой; это число радианов, на которое фаза изменяется за 1 сек. Она определяется дифферен­циальным уравнением. Другие величины уравнением не опре­деляются, а зависят от начальных условий. Постоянная а слу­жит мерой максимального отклонения груза и называется ам­плитудой колебания. Постоянную D иногда называют фазой колебания, но здесь возможны недоразумения, потому что другие называют фазой w 0t+D и говорят, что фаза зависит от времени. Можно сказать, что D — это сдвиг фазы по сравнению с некоторой, принимаемой за нуль. Не будем спорить о словах. Разным D соответствуют движения с разными фазами. Вот это верно, а называть ли D фазой или нет — уже другой вопрос.

§ 3. Гармоническое движение и движение по окружности

Косинус в решении уравнения (21.2) наводит на мысль, что гармоническое движение имеет какое-то отношение к движению по окружности. Это сравнение, конечно, искусственное, потому что в линейном движении неоткуда взяться окружности: грузик движется строго вверх и вниз. Можно оправдаться тем, что мы уже решили уравнение гармонического движения, когда изуча­ли механику движения по окружности. Если частица движется по окружности с постоянной скоростью v, то радиус-вектор из центра окружности к частице поворачивается на угол, величина которого пропорциональна времени. Обозначим этот угол q =vt/R (фиг. 21.2).

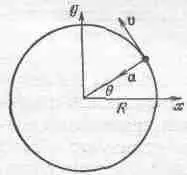
Фиг. 21.2. Частица, движу­щаяся по кругу с постоянной скоростью.

Тогда d q /dt= w 0 =v/R. Известно, что ускоре­ние а=v 2/R=w 2 0R и направлено к центру. Координаты движу­щейся точки в заданный момент равны

Читать дальше