Владимир Живетин - Экономические риски и безопасность (анализ, прогнозирование и управление)

10. Область критических состояний Ω кри соответствующие ей х кризменяются в процессе функционирования динамической системы и определяются опытным путем или теоретически.

11. Для управления системой используют измеренные значения контролируемых параметров, которые обозначим х изм.

12. Для предотвращения потерь и наилучшего достижения цели динамическая система имеет системы контроля и управления. С помощью систем контроля, обладающих погрешностями, в процессе функционирования динамической системы вычисляют (строят) Ω 0 доп. При этом, как правило, Ω допне совпадает с Ω 0 допза счет погрешностей δx функционирования систем контроля.

13. На выходе динамической системы реализуются текущие или фактические значения параметров, которые обозначим х ф. При этом х изм= х ф + δх, где δх – погрешность измерения, в общем случае случайный векторный процесс.

14. Фактические значения параметров х фв силу объективных причин, обусловленных внешними и внутренними возмущениями, а также свойствами человека, изменяющимися случайным образом, представляют собой в общем случае случайные процессы. На этапе проектирования динамической системы векторный процесс х фопределяется с помощью математических моделей.

15. Для компенсации влияния δх на величину риска вводятся допустимые оценочные значения параметров х 0 допи соответствующая им область Ω 0 доп 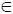Ω доп, т. е. вводится запас Δ = (х доп – х 0 доп). При контроле динамических процессов, когда 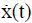≠ 0 (скорость изменения процесса во времени), необходимо вводить дополнительный запас Δ 1= k 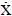, и тогда x дин доп= x доп– k 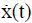. В результате имеем: область Ω 0 допвключена в Ω дин доп, которая включена в область Ω доп, т. е. х 0 доп≤ x дин доп≤ x доп(рис. 3.11).

16. Предотвращение потерь состоит в обеспечении условия x ф(t) 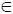Ω доп(t) для любого момента времени t функционирования динамической системы. Для целей управления имеем х изм, кроме того, система контроля индуцирует оператору не Ω доп, а Ω 0 доп. При этом х доп= х доп+δх доп, где δх доп – погрешность функционирования системы контроля, x 0 доп 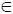Ω 0 доп. В этих условиях мы можем обеспечить только x изм 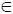Ω 0 доп, а это значит, что возможен выход х физ области Ω доп, что означает соответствующие потери и риск.

17. В силу того, что процессы х фи х измявляются случайными, в качестве меры риска будем рассматривать вероятности Р i 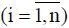событий, приводящих к потерям.

18. С учетом сказанного необходимо разработать показатели экономического риска и безопасности вида

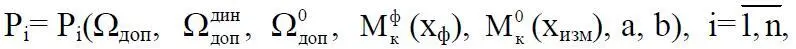
где М ф к(х ф) – момент k-го порядка случайного векторного процесса х ф; М 0 к(х изм) – момент k-го порядка случайного векторного процесса х изм; а, b – параметры системы, векторные величины.

19. В дальнейшем экономический риск будем характеризовать как вероятность неадекватного отображения окружающей, прежде всего экономической, среды, в результате чего параметры х i, подлежащие контролю и ограничению, принимают значения x i 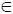Ω кр, т. е. принадлежат критической области.

20. Экономическую безопасность будем характеризовать вероятностью выполнения условия x 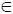Ω доп, т. е. принадлежности контролируемого индикатора допустимой области состояний.

21. Полученные расчетным путем Р i 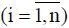уточняются в процессе функционирования динамической системы. При этом уточняются как P i, так и Ω доп.

II. Решение задачи.

Экономический риск будем оценивать величиной вероятности выхода фактических состояний динамической системы из области допустимых состояний [9]. Таким образом, мы хотим выделить те ситуации, которые ведут к потерям, т. е. связаны с риском. Для анализа процесса введем гипотезы В 1и В 2.

Гипотеза В 1.Фактическое состояние динамической системы находится в области допустимых состояний, т. е. x ф 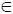Ω доп.

Гипотеза В 2 . Хотя бы один параметр-индикатор динамической системы имеет фактическое состояние, которое находится вне допустимой области, т. е. (x ф) i 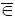Ω доп.

При этих двух гипотезах система контроля формирует две модели А 1и А 2, представленные в виде двух сигналов-событий

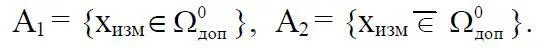
Ситуация, когда справедлива гипотеза В 1и выполняется событие А 1, соответствует такому функционированию экономической системы и используемых им систем контроля, при которых цель ее функционирования выполняется, т. е. нет потерь, нет риска. Вероятность пересечения этих событий обозначим через P 1= P(B 1∩ A 1), которая оценивает безопасное состояние.

В случае, когда реализуются гипотеза В 1и событие А 2, в системе контроля создается ложное представление (оценка) о состоянии динамической системы, и эта оценка создается по причине возникновения δx. Вероятность такого события P 2= P(B 1∩ A 2).

Рассмотрим гипотезу В 2и событие А 2. Эта ситуация соответствует такому состоянию динамической системы, при котором цель не выполняется, так как фактическое значение x фнаходится вне области допустимых состояний. Такая ситуация обусловлена как ошибками системы контроля δx, так и неопределенностью внешней информации 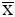. Вероятность этого события обозначим P 3= P(B 2∩ A 2).

Событие B 2∩ A 1означает, что фактическое состояние контролируемого объекта находится вне области допустимых состояний, риск велик, а система контроля указывает человеку, что все в порядке, и динамическая система достигает цель, риска нет. Обозначим вероятность этого события P 4= P(B 2∩ A 1). На рис. 3.12 представлена диаграмма событий В i, A j(i = 1,2; j = 1,2).

Для решения задачи анализа необходимо установить связь между вероятностями Р i 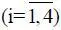, допустимыми значениями векторов x ф, 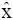= x изм, а также плотностями вероятностей векторов x фи 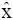= x изм. С этой целью, учитывая определения