Владимир Живетин - Экономические риски и безопасность (анализ, прогнозирование и управление)

Распространим данный пример в область сбыта. Предположим, что имеется одно управление, один менеджер, в рассматриваемой системе (фирме), стране, который обеспечивает сбыт изготовленной продукции. Пусть фирма имеет n точек реализации товара. Предположим, на основании информации I i 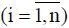из точек реализации товара менеджер принимает решение об отправке товара в эти точки. Предположим также, что в процессе реализации в m 1точках товар реализовался, и мы получили прибыль, а из m 2точек пришла ошибочная информация, товар там залежался и испортился. В m 3точек на основании информации I 3менеджер не послал товар, предполагая, что он не может быть реализован. Но оказалось, что это не так, и здесь фирма тоже понесла потери. В m 4точках, зная на основании информации I 4о невозможности реализации товара, мы его все-таки послали, получив в итоге потери. При этом мы имеем: n = m 1+m 2+m 3+m 4, а итоги деятельности по реализации товара можно оценить следующими величинами – частотами:

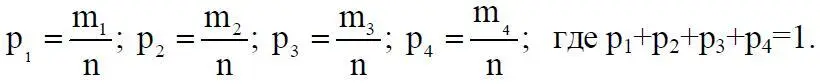
Величина p 1характеризует (численно) безопасные операции по реализации товара; p 2 – (численно) величину (частоту) потерь товара. Величина p 3есть частота потерь в реализации товара, обусловленная нашим отказом. Величина p 4 – частота потери реализации товара из-за непреодолимых ситуаций. При этом p 2, p 3, p 4 – частоты потерь, которые несет фирма, отнесем к категории риска, а частота p 1 – есть характеристика безопасных реализаций, в некотором смысле безопасного состояния экономики данной фирмы.

Изменяя объем, достоверность и регулярность информации I i 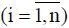о состоянии рынка в рассматриваемых i-х точках, мы можем изменить значения m i(i = 1,2,3,4). При этом, увеличивая объем, достоверность и регулярность I i, мы можем увеличить m 1и уменьшить m 2, m 3, m 4. Однако при этом возрастает стоимость товара за счет увеличения стоимости информации I i. В связи с этим уменьшение m 2 + m 3 + m 4, с одной стороны, уменьшает потери и, соответственно, риск, но при увеличении стоимости товара потери возрастают. Все это обуславливают необходимость анализа численных величин, связанных как с p i 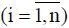, так и с изменением стоимости товара и не только по причине возрастания стоимости информации, но и других возмущающих факторов как внешнего, относительно фирмы, так и внутреннего происхождения.

Цель управления в макроэкономике. В общем случае на выходе макроэкономической системы или ее отдельных подсистем имеет место некоторый процесс х, зависящий от времени, т. е. x = x(t). Его фактическое или истинное значение мы будем обозначать х ф(t) (рис. 3.10). В силу влияния внешних и внутренних возмущающих факторов, действующих на систему, этот процесс мы будем относить к случайным. Это предположение позволит нам воспользоваться известными, достаточно глубоко разработанными положениями теории случайным процессов. При этом для x фможно записать: х ф= m х + Δх, где m x= m x(t) – математическое ожидание х, в общем случае функция времени; Δx = Δx(t) – отклонение фактического значения x фот его математического ожидания.

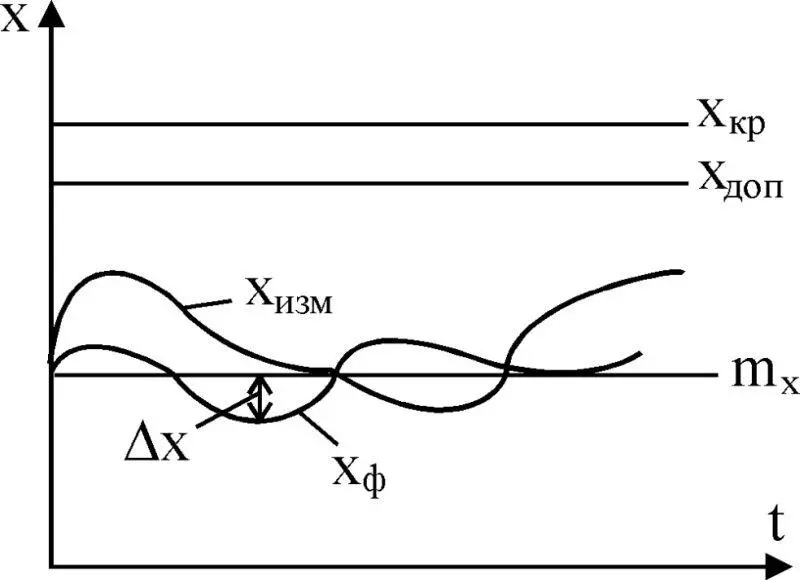
Рис. 3.10

Задачей подсистемы управления является формирование такого управления на основе информации, поступающей от подсистемы контроля в виде измеренного (х изм), допустимого (х доп), критического (х кр) значений одного x iили всей совокупности компонент вектора x – индикаторов х 1, …, х n, при котором обеспечивается ее безопасное состояние, т. е. состояние, при котором индикаторы x i 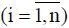системы находятся в допустимой области: x 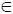x доп. Указанная цель экономики достигается с помощью управления, если нам известны x кри x доп. В рамках рассматриваемой ниже теории мы можем сформулировать задачу.

По известной величине x кр, заданных статистических характеристиках Δx фактического и истинного значений x ф, заданных погрешностях измерения фактического значения x ф, рассчитать допустимое значение x измдля параметров, подлежащих ограничению. Таким образом, x крдолжно быть задано из дополнительных соображений.

С какой целью мы вводим величину x доп< x кр? Рассмотрим это обстоятельство, используя материалы предыдущих глав. Начнем с примера.

Пусть нами рассматривается индикатор состояния экономики x, критическое x крзначение которого нам известно. Это значит, что при всех x < x крэкономика по данному индикатору находится в области безопасного состояния. Согласно существующим правилам, когда отсутствуют погрешности измерения, мы осуществляем измерение x и сравнение x кри x изм. Как только x изм= x кр, формируется управление u(t), направленное на уменьшение x(t). Если такое управление может быть сформировано и реализовано, мы достигли цели, обеспечив безопасное состояние экономики.

Ситуация меняется, когда измеренное значение x дает нам информацию о фактическом значении x с погрешностью, а сам процесс x(t) – случайный. Как показано выше, данная ситуация имеет место для ВВП как в США, так и в РФ. Если управление u(t), направленное на ограничение x(t), мы будем формировать из условия z < x кр, то за счет погрешностей δx(t) измерения не исключена ситуация, с какой-то долей вероятности, когда x > x кр, т. е. система будет находиться в области опасного состояния.

Согласно материалам главы II, для России предложено критическое значение ВВП не меньше 75 % от ВВП, например, США. Предположим, что мы составляем в декабре планы на следующий год. Для того, чтобы найти (x 1) кр, т. е. критическое значение ВВП в РФ, нам нужно путем расчетов вычислить потенциальный ВВП, как это делают в экономике США. Обозначим полученное значение через x 0 1. Тогда (x 1) крдля РФ есть величина 0,75x 0 1, т. е. (x 1) кр= 0,75x 0 1, которая задает область Ω кр. Методика расчетов x 0 1не включает погрешности измерения δx, внешние w(t) и внутренние v(t) возмущающие факторы, например, в виде случайных величин или процессов. Если мы будем учитывать δx, v, w, то нам необходимо вводить иную область, обозначим ее Ω доп, которая будет меньше, чем Ω кр. При этом мы используем различные критерии. При расчете x крмы используем детерминированные объекты и для назначения Ω криспользуем критерии, которые называют первичными [11].

Вслед за первой задачей построения Ω допвозникает вторая: как осуществить и сформировать управление, при котором x не выходит из области Ω доп? На локальном, малом отрезке времени экономические системы, как правило, неизменны, и поэтому их можно описать, например, в виде статической математической модели. Эта модель будет соответствовать только этому моменту времени t 0, и все выводы, полученные на основании этой модели, можно использовать только при t = t 0.