Владимир Живетин - Технический риск (элементы анализа по этапам жизненного цикла ЛА)

2) статистические описания характеристик модели или измерения ее параметров;

3) проверка статистических гипотез;

4) построение итоговой модели М, включая подгонку модели;

5) анализ свойств модели М;

6) статистическое моделирование на полученной модели М.

Одна из причин отличия реальной математической модели М 2, принятой в расчетах, от идеальной М 1, которая описывает функционирование реального объекта без погрешностей, состоит в том, что идеальная модель для расчетов упрощается. Это упрощение происходит по различным причинам и, в частности, из-за невозможности применить М 1при расчетах на этапе НИР из-за ее сложности. Рассмотрим пример такого упрощения и допускаемые при этом погрешности.

Пусть создана математическая модель М 1, которая представляет собой систему из n уравнений, заданная в пространстве R Nс координатами x = (x 1, x 2, …, x N), вида

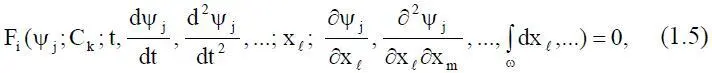
где 1 ≤ i ≤ n; 1 ≤ l, m ≤ N, 1 ≤ k ≤ α; x, t – соответственно пространственные и временные переменные.

Таким образом, (1.5) представляет собой систему интегро-дифференциальных уравнений для объекта с распределенными параметрами. Решения ψ j= ψ j(t,x;C k) описывают состояние объекта или системы в некоторый момент времени t, поэтому их называют переменными состояниями. При этом предполагается, что уравнения F i= 0 зависят от параметров C k, например, числа Маха (М), числа Рейнольдса в авиации, структурных констант, которые могут влиять на свойства решений ψ j, поэтому их называют управляющими параметрами.

Проблема исследования решений системы уравнений (1.5), даже если речь идет лишь о том, как зависят эти решения от управляющих параметров С k, является исключительно сложной. По этой причине вводится ряд последовательных предположений, каждое из которых вносит соответствующие погрешности. К числу таких предположений относятся изменения в структуре модели М:

1. Погрешность δ 11, обусловленная пренебрежением элементов объекта, описываемых интегралами. В результате модель (1.5) заменяется новой моделью вида

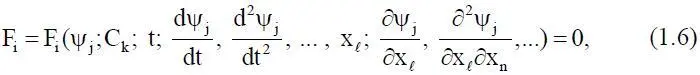
которая представляет собой систему нелинейных уравнений в частных производных.

2. Погрешность δ 12, обусловленная новым упрощающим предположением, согласно которому модель не содержит пространственных производных любого порядка, т. е.

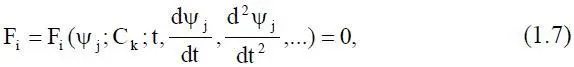
которая описывает объект с сосредоточенными параметрами.

3. Погрешность δ 13, обусловленная переходом от модели (1.7) к модели вида

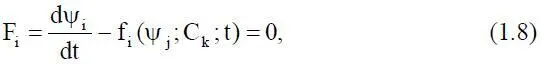
когда модель содержит производные не выше первого порядка и, кроме того, эти производные входят в упрощенную функцию F iспециальным каноническим образом. Систему уравнений F i= 0 называют динамической системой.

4. Погрешность δ 14, обусловленная предположением, что функция f iв (1.8) полностью не зависит от времени, тогда получаем модель

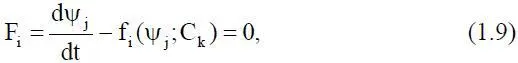
которая называется автономной динамической системой. Для таких систем, когда k ≤ 4, имеются некоторые интересные результаты в области свойств решений.

5. Погрешность δ 15, обусловленная переходом от (1.9) к системе вида

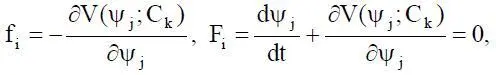
когда все функции f iмогут быть заданы антиградиентом по отношению к ψ iнекоторой потенциальной функцией V(ψ j; C k). Свойства таких систем изучены довольно глубоко.

6. Погрешность δ 16, обусловленная переходом к модели, описывающей состояния равновесия dψ i/dt = 0 градиентных динамических систем. В этом случае модель изучаемого процесса принимает вид

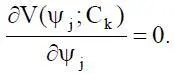
Эти уравнения могут не иметь решений, если V(ψ) = ψ; иметь одно решение при V(ψ) = ψ 2; более, чем одно решение, если V(ψ,c) = ψ 4+ cψ 2: при c < 0 – имеется три решения, а при c > 0 – одно решение. При этом задача исследования заключается в том, каким образом состояние равновесия ψ j(C k) потенциальной функции V(ψ j;C k) изменяется при изменении управляющих параметров C k.

Среди других методов исследования системы, основанных на переходе от (1.5) к более простым моделям, что обуславливает погрешности типа δ 1j, рассмотренные выше, укажем:

1) метод линеаризации;

2) вариационные методы;

3) метод прогонки или метод начальных параметров.

Важным моментом в этих методах является приближенная замена дифференциальных уравнений (1.6) в частных производных системой обыкновенных дифференциальных уравнений, характеризующих динамические свойства системы с конечным числом степеней свободы.

Пусть рассматриваются абстрактные вероятностные или статистические модели физических объектов. Модель исследуемого объекта и модель полученных данных отличны. Эти отличия обусловлены тем, что экспериментальные данные отражают не только состояния изучаемого объекта, значения его характеристик и параметров, но и условия проведения, связанные с внешними возмущающими факторами δ 1, а также упрощения и допущения, использованные при обработке эксперимента δ 2. Если первые связаны с внешней средой, то вторые – со структурой объекта, с ее упрощением, которые проявляют себя в моделях, алгоритмах, построенных на основе экспериментальных данных.

Рассмотрим подробнее этот процесс, в основу которого положен морфологический анализ, широко используемый при исследовании и проектировании различных технических объектов [11]. Разберем задачу измерения характеристик случайных процессов, т. е. первый этап построения модели, например, в форме дифференциальных уравнений, позволяющих прогнозировать состояние изучаемого объекта, исследовать его устойчивость, прогнозировать численную величину показателей риска. Этапы таких работ включают следующие погрешности:

1. Получение исходных данных: принцип получения исходных данных (ансамблевый или траекторный) и оператор усреднения, а также количество обращения к исходным данным – погрешности δ 21.

2. Схема сравнения с образцовой величиной: количество сравнений (одно или несколько) представляет собой этап, в котором производится сравнение измерительных преобразований; вычислительные преобразования – погрешности δ 22.