Владимир Живетин - Технический риск (элементы анализа по этапам жизненного цикла ЛА)

3. Схема дискретизации траектории по времени: непрерывная; дискретная – погрешность δ 23.

4. Схема квантования значений реализаций по уровню: без квантования (непрерывнозначный; аналоговый); с квантованием всех значений (цифровой); с квантованием части значений – погрешность δ 24.

5. Добавление вспомогательных сигналов – погрешность δ 25.

6. Преобразование по формулам оценивания – погрешность δ 26:

– количество значений, используемых в качестве результата измерения одной величины (одноинтервальный – две точки) – δ 261;

– способ оценивания (параметрический, непараметрический) – δ 262;

– объем исходных данных (фиксированный или переменный) – δ 263;

– принцип реализации вычислительных операций (детерминированный, стохастический) – δ 264;

– принцип организации вычислительного процесса (формул связи текущего значения с предшествующим): одношаговый; многошаговый – δ 265;

– метод вычислений: с фиксированным числом операций; с переменным числом операций – δ 266;

– вид измеряемой величины (скалярный, векторный): детерминированная, постоянная; реализация случайного элемента (байесовский) – δ 267;

– суммарная погрешность на данном этапе имеет вид: .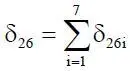

7. Схема изменения аргумента модели в процессе усреднения: аргумент остается постоянным; аргумент изменяется по заданному закону – погрешность δ 27.

8. Получение конечного результата: непосредственно по исходным данным (прямой); пересчетом результатов измерения других характеристик, т. е. косвенным методом – погрешность δ 28.

9. Аналитическое описание результатов измерения: без аналитического описания; с аналитическим описанием – погрешности δ 29.

10. Учет априорных и апостериорных данных: наличие адаптации (без и при наличии) к априорным и апостериорным (первичным, вторичным) данным – погрешности δ 210.

Суммарная погрешность модели физической системы, которую мы заложили при построении ее математической модели в процессе эксперимента, записывается в виде

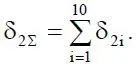
Предположим, что построена математическая модель случайного процесса, т. е. построен, например, алгоритм, связывающий выходной процесс x(t) с входным процессом y(t), характеристики которого заданы в виде x(t) = ψ(y(t),δ 2i), где ψ – оператор преобразования. Наличие погрешностей δ 2iзаставляет нас искать показатели качества алгоритма, которые являются характеристикой соответствия алгоритма его назначению, т. е. пригодность алгоритма для получения решения поставленной задачи и близость достижения цели.

Рассмотрим критерий применимости упрощенных математических моделей изучаемых динамических систем. Зададим Р 1, Р 2и Р 3Предположим, х = m х+ Δx, где m х – математическое ожидание х; Δx – отклонение х от его среднего значения (m x). В этом случае вероятность Р 1можно записать так [6]:

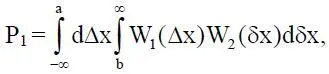
где а = х в доп – m x; b = х о доп – m x – δx; W 1, W 2 – плотности вероятностей Δх, δх.

Выбирая ту или иную модель М 2, мы изменяем W 2(δх), оставляя W 1(Δх) неизменной. Можно показать, что при возрастании дисперсии σ 2(δх) условие Р 1= const выполняется, если запас Δ = х доп – х о д опувеличивается. Очевидно, что существует то значение σ 2(δх), при котором Δ очень велико и эффективность применения такого объекта недопустимо мала (рис. 1.18).

Рис. 1.18

Таким образом, переход к упрощенной модели при проведении НИР приводит к уменьшению области допустимых состояний ограничиваемого параметра х.

Задача разработчика проекта: наложить ограничения на Δ и принять ее равной Δ*. Все модели, для которых Δ ≤ Δ*, будут допустимы для целей анализа и синтеза. Таким образом, проблема анализа риска и управления им включает в себя: построение плотностей вероятностей фактических х ф= m x(t) + Δx(t) и измеренных (оценочных) х изм= х ф(t) + δх(t) значений процессов, подлежащих контролю и ограничению. Для построения плотностей вероятностей W 1(x ф) или W 1(Δx), а также W 2(x изм) или W 2(δx) необходимы соответствующие математические модели. Построению таких моделей посвящена данная работа.

Для расчета технического риска необходимо иметь плотность вероятностей ограничиваемых параметров, представляющих собой, как правило, случайные процессы. Для аналитического построения искомых плотностей вероятностей необходима математическая модель случайного процесса, а также внешних и внутренних возмущающих факторов. Для решаемой задачи математическая модель движения самолета представляет, в достаточно общем виде, систему нелинейных дифференциальных уравнений, на вход которой поступает белый шум [6]. При этом на выходе системы (модели) получают многомерный марковский процесс, что существенно упрощает нахождение плотностей вероятностей W(·) аналитическим методом. С этой целью используется математический аппарат уравнений Фоккера-Планка-Колмогорова (ФПК). Однако при размерности вектора x(t) ограничиваемых параметров больше трех, решение ФПК-уравнения представляет собой трудноразрешимую задачу. В этом случае используют различные процедуры, упрощающие вычисления W(x i,t), где x i – процесс, подлежащий контролю, ограничению и прогнозированию, т. е. вычислению x i(t + Δt), где Δt > 0, а также моделированию его с помощью известных технических средств.

Пусть задана техническая система (объект), на выходе которой возможна регистрация процесса x i= z(t). Требуется построить математическую модель процесса z(t). Пусть поставлен эксперимент, в котором измерены значения z(t) с погрешностями δ 2Σ, в результате получено z(t) = z ф+ δ 2Σ, где z ф – фактическое значение z(t); для z(t) построены одномерная плотность распределения ω(z) и корреляционная функция B z(τ). Построение математической модели процесса z(t) осуществляется в три этапа.

На первом этапе производится аппроксимация одномерной плотности распределения ω(z) изучаемого процесса z(t) плотностью S-распределения Джонсона [19, 20]. При этом исключаются из рассмотрения те процессы, которые не могут быть аппроксимированы указанным образом. Поскольку класс плотностей S-распределения Джонсона образован тремя семействами (S B, S Uи S L-распределения), то аппроксимация распределений ω(z) заключается в выборе соответствующего семейства плотностей S-распределения и в определении его параметров. Процедура такой аппроксимации описана в работе [6]. Следует только добавить, что исходной информацией для аппроксимации являются первые четыре момента распределения процесса z(t), которые, в общем случае, следует предварительно вычислить. Для некоторых видов плотности распределения ω(z) эти моменты указаны в справочной литературе. После того, как для ω(z) определено соответствующее S-распределение, для построения математической модели искомого процесса z(t) необходимо описать нормированный гауссовский процесс y(t) и подвергнуть его нелинейному преобразованию Джонсона. Указанное преобразование будет иметь вид